MBA流エクセル術【ソルバー編】 – ビジネスに使えるテンプレート配布

前回、予想を大きく上回る反響をいただいた『【MBA流】エクセル “超” 基礎講座 ビジネスに使えるテンプレート配布』（詳しくは下記ツイートをご確認ください）ですが、今回はその第2弾をお届けします！

【無料配布：エクセル “超” 基礎講座】

UCLAで学部生向けの『エクセル “超” 基礎講座』の資料をまとめたのですが、欲しい方いますか？

実際に受講すると8万円程度の内容です。

✅損益計算書の試算
✅新規顧客獲得数の予測
✅価格計算

いいね＆RT頂いた方にはDMで送ります！
※フォロワーさん限定 pic.twitter.com/PiCn5E6F1L

— Yusaku@ UC San Diego － 【MBA流】Eコマースビジネスのノウハウ公開中 (@yusaku_nakamura) April 30, 2021

みなさん、こんな悩みありませんか？

この記事は、UC San Diego のMBAで実際に教えられている授業『Spreadsheet Modeling』を私がまとめたものです。（授業ではソルバーの基本から応用までを学びますが、今回は基本の部分に焦点を絞って解説しました）

ソルバー自体はやや難易度の高い機能ですが、エクセル初心者にもわかりやすいように83枚の画像付きで解説しています！この記事を読むと、以下のことが理解できるようになります。

実際に受講すると8～10万円の内容になります。

エクセルのテンプレートは以下のツイートから無料配布していますので、合わせてご確認ください。

【Excel無料配布 第2弾】

MBAで実際に教えられた『Excel ソルバー入門』をまとめた資料、欲しい方いますか？

第1弾(下記引用RT)と合わせ実際に受講すると約16万円相当の内容です

✅利益最大化の試算
✅コスト最小化
✅感度レポートの理解

いいね＆RT頂いた方にDMで送ります！
※フォロワーさん限定 https://t.co/wDLy3Nm9Fh

— Yusaku@ UC San Diego － 【MBA流】Eコマースビジネスのノウハウ公開中 (@yusaku_nakamura) May 22, 2021

また、前回の第１弾は『【MBA流】エクセル “超” 基礎講座』について記事を書いていますので、興味がある方はぜひご覧ください。第３弾はPower Query、Power Pivotの使い方・テンプレートを配布する予定ですのでお楽しみに♪

それでは早速はじめましょう！

MBAでエクセルを教える理由

私がMBA留学していた大学（UC San Diego）に限らず、米国のMBAでは、たかがエクセルの基本操作と簡単なモデリングを教えるためだけに有名教授やコンサルタントをわざわざ呼び寄せ、数日間みっちりと講義をします。（UCSDの場合は費用にすると、生徒1人当たり１日8万円 × 4日 = 32万円です！！）

なぜでしょうか？それはコンサルや投資銀行に勤めると、ファイナンスや経理、マーケティングやサプライチェーンなどの分野で複雑なシミュレーションモデルを作る際、まだまだエクセルが主流なのです。プログラミングが必須のスキルになってきたとはいえ、並行してエクセルの機能も進化し続けており、実際にアメリカで1兆円を超える大企業でも現場ではエクセルが活躍しています。

ということで、全３回に渡り『MBAで教えられたエクセル術』を余すところなく解説するシリーズ、今回は第２弾をお届けします！今回の【ソルバー編】では、限られた資源で利益を最大化するエクセルのモデリングを理解することができます。身につけるかどうかはあなた次第です！

エクセルのソルバーとは？

エクセルの分析ツールに『ソルバー』という機能があるのをご存知でしょうか？あまり聞きなれない言葉かも知れません。MBAではこのソルバーの使い方の基本から応用までを一通り学びます。実は、私たちの日常生活や中小企業の経営者の意思決定ツール、大企業の実際のビジネスでもソルバーは以下のようなところで使われています。

ソルバーの使い方を理解すれば、Excelマクロの機能は一切使わずに、上記の問題の答えが一瞬で出せるようになります。

エクセル　ソルバーの設定方法

まずはエクセルでソルバーを使うための設定をしましょう。３分くらいでできますよ！

パソコンでエクセル（Microsoft Excel）を起動し、エクセル上部の『データ』をクリックして、下図のように『ソルバー』メニューが表示されるかどうか確認します。

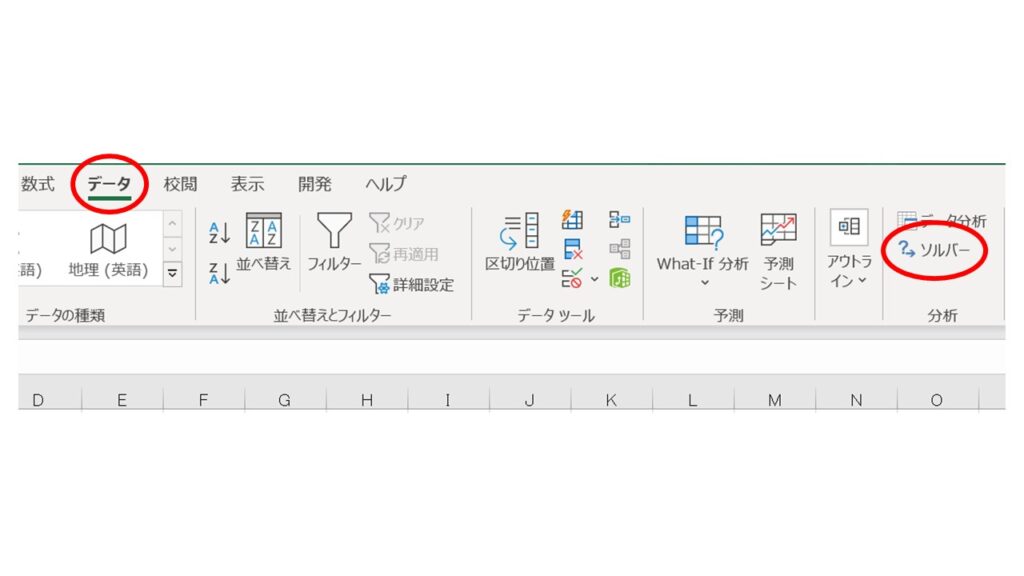
多くの方はソルバーを使ったことがないと思うので、ソルバーメニューは表示されていないと思います。その場合は、エクセル上部の『ファイル』→『その他』→『オプション』でエクセルのオプション画面を出します。

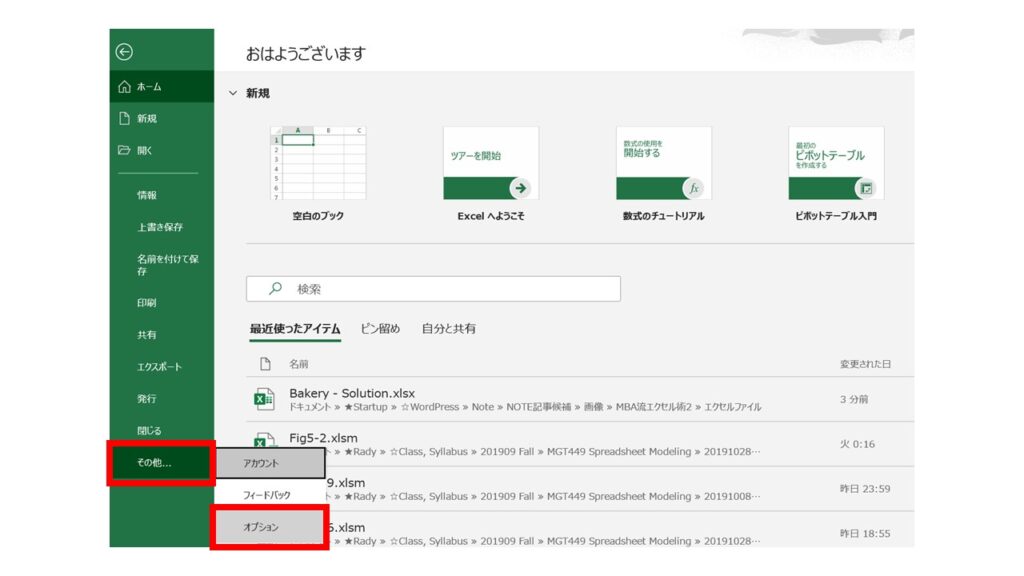
『Excelのオプション』ウィンドウが表示されたら、左メニューから『アドイン』をクリックしてください。

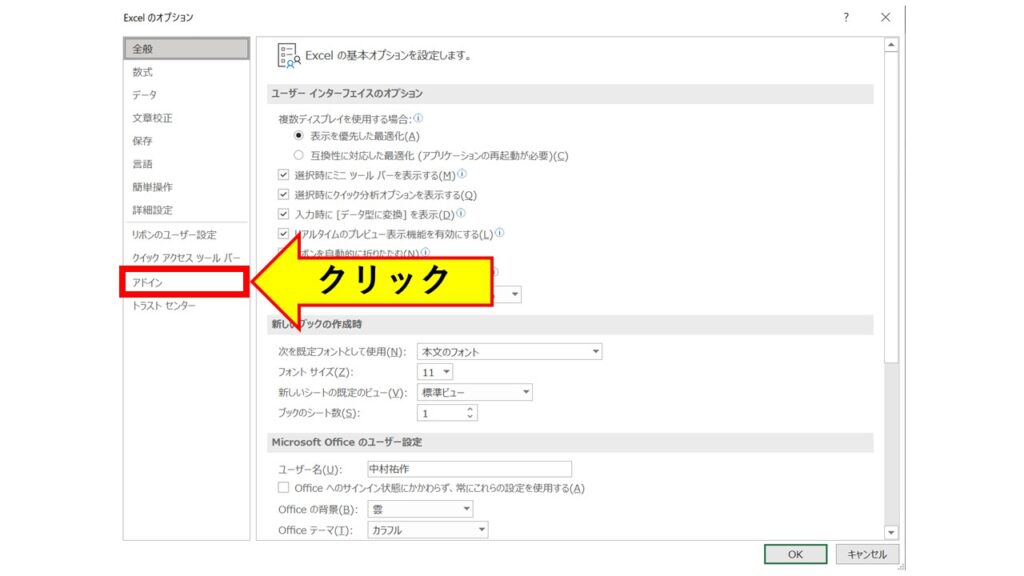
アドインのアプリケーションの中に『ソルバー アドイン』があることを確認してください。そして、ウィンドウの下方にある［管理］が『Excelアドイン』になっていることを確認して、『設定』ボタンをクリックします。

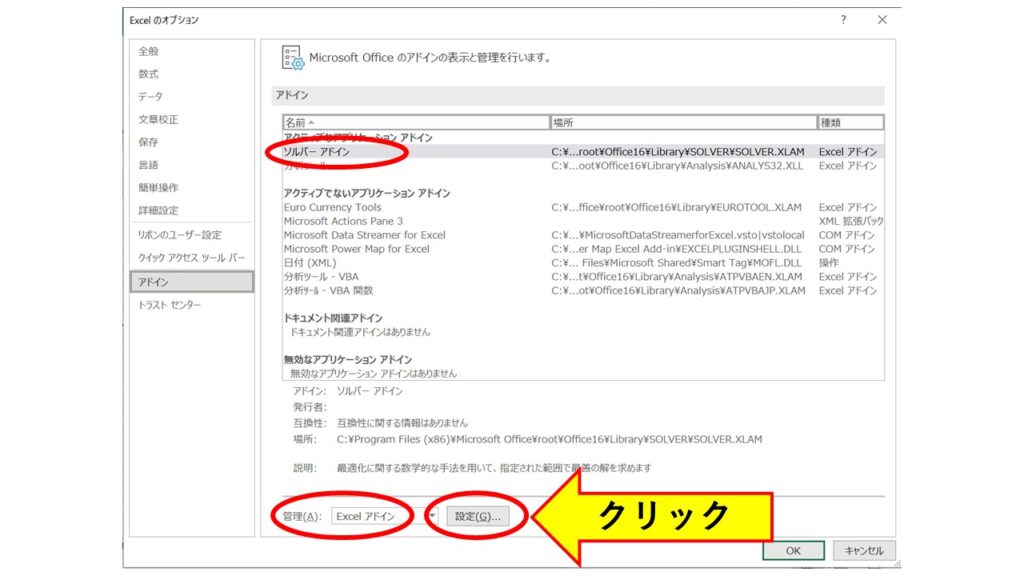
『アドイン』ウィンドウが開きますので、『ソルバーアドイン』のチェックボックスをオンにして『OK』ボタンをクリックしてください。

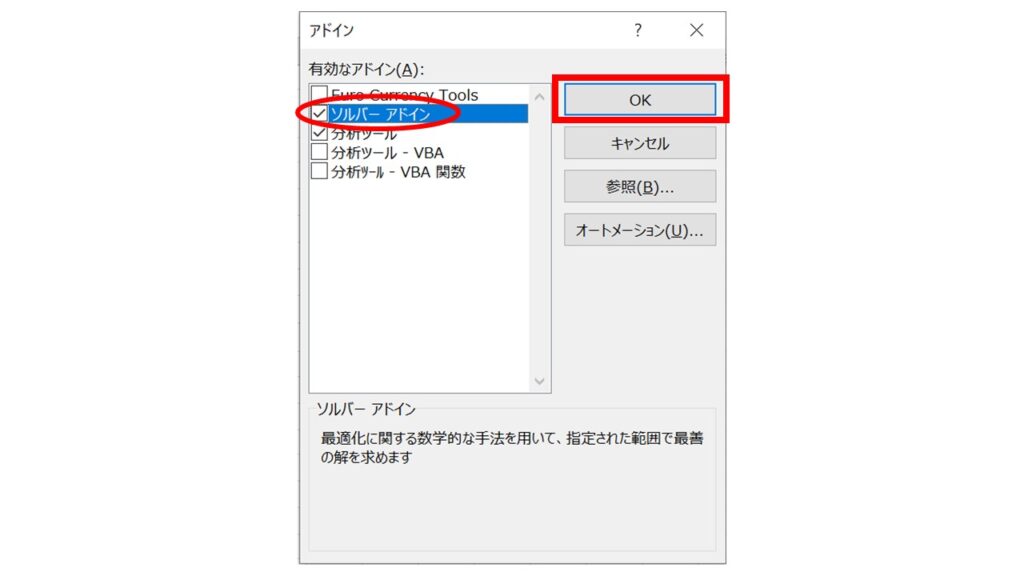
これでエクセルに戻ると、エクセル上部の『データ』をクリックすれば、下図のように『ソルバー』が表示されると思います。これで設定完了です！簡単ですね！

モジュール１：ソルバーの基本操作

まずは例題を使ってソルバーの基本操作から解説します。ここでは最大値の求め方について考えてみましょう。

できること：ソルバーの基本的な使い方がわかる

このエクササイズでは、ソルバーの基本的な使い方を学ぶことができます。まずはソルバーの操作を理解しましょう。例題１の図を見てください。

例題１

XとYの条件が以下で与えられています。

このとき、X + Y の最大値はいくつになるでしょうか？
条件がこれだけならソルバーを使わなくても計算できますね。X = 5、Y = 3 のときが最大で、
X + Y の最大値は８です。

ソルバーの基本『３ステップ』

これを『３ステップ』でエクセルのソルバーで表現してみましょう。ソルバーの３ステップは以下の通りです。

ステップ１：『変化するもの（=変数）』を決める

今回の場合、変数はXとYの２つですね。まずは下記エクセルの “水色セル” のように ”X” と ”Y” を定義します。（C3セルを ”X” 、D3セルを ”Y” と定義する）

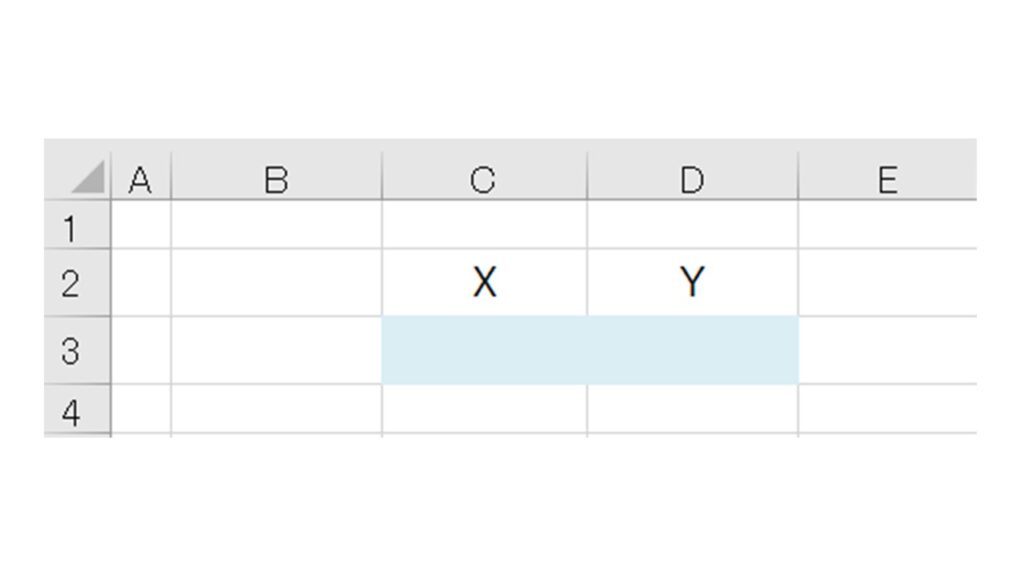
ステップ２：最終的に『求めたいもの』を決めて、計算式を入力する

次に『求めたいもの』を定義します。今回の場合は ”X + Y” の最大値が求めたいものですね。
したがって下記の ”黄色セル” を、”求めたいものを計算させるセル” に指定して、計算式（X + Y）を入力します。（F4セルに “=C3+D3” を入力しました）

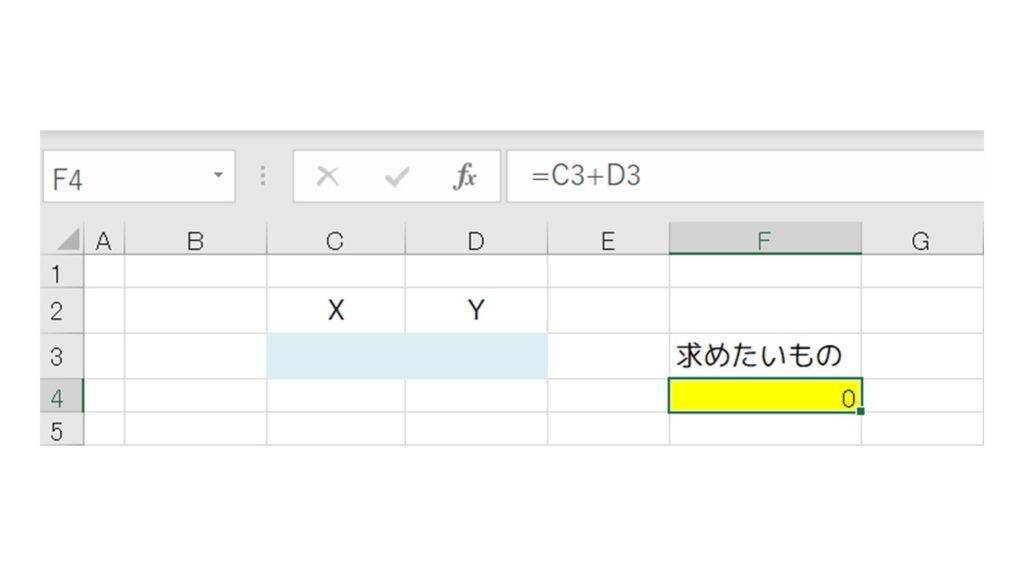
ステップ３：『制約条件』を入力する

最後に『制約条件』を定義します。下記の ”水色セル” の通り、 XとYの条件である “3≦X≦5”、 “Y≦3” を定義します。（D7セルにXの値、つまり “=C3” を入力します。同様に、D8セルにYの値、つまり “=D3” を入力します。）

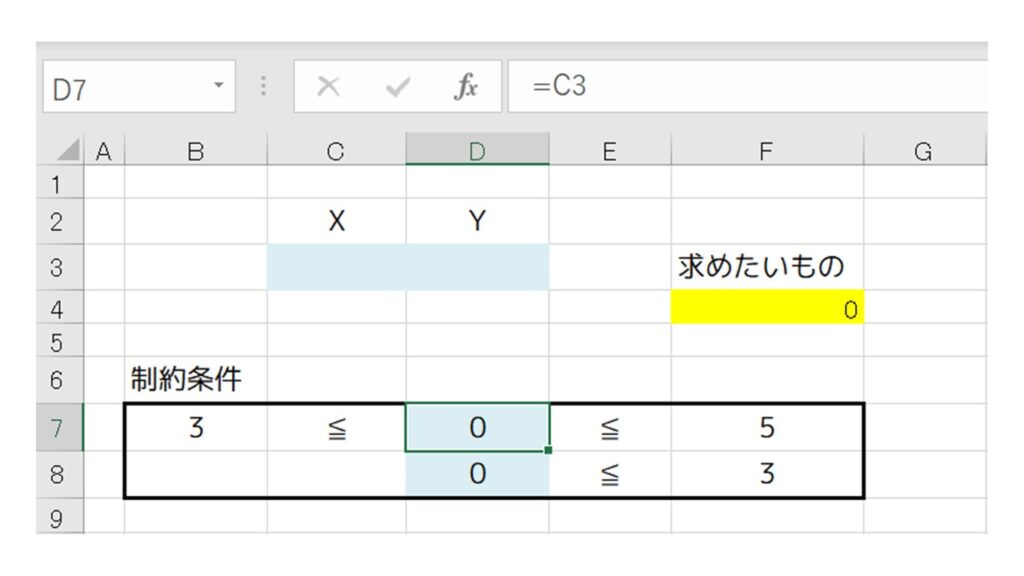
これでエクセル入力の準備は完了です。あとはソルバーを起動しましょう。エクセル上部の『データ』→『ソルバー』をクリックします。

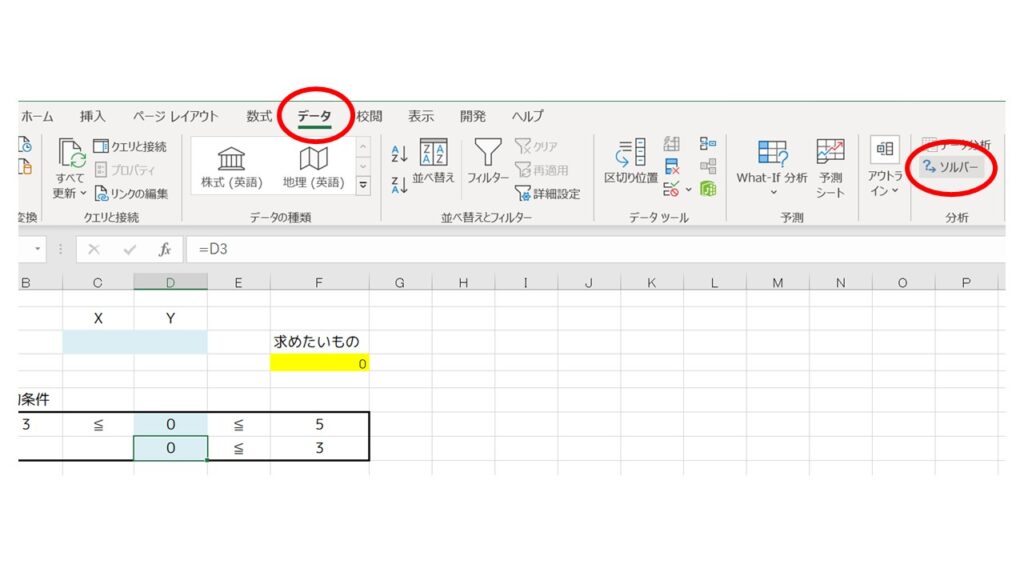
『ソルバーのパラメーター』というウィンドウが開きますので、セルを指定していきます。まずは、目的セルの設定に、求めたいものである『F4』セルを指定します。（右にある『矢印マーク』をクリックするとセルが指定できるので便利です。）

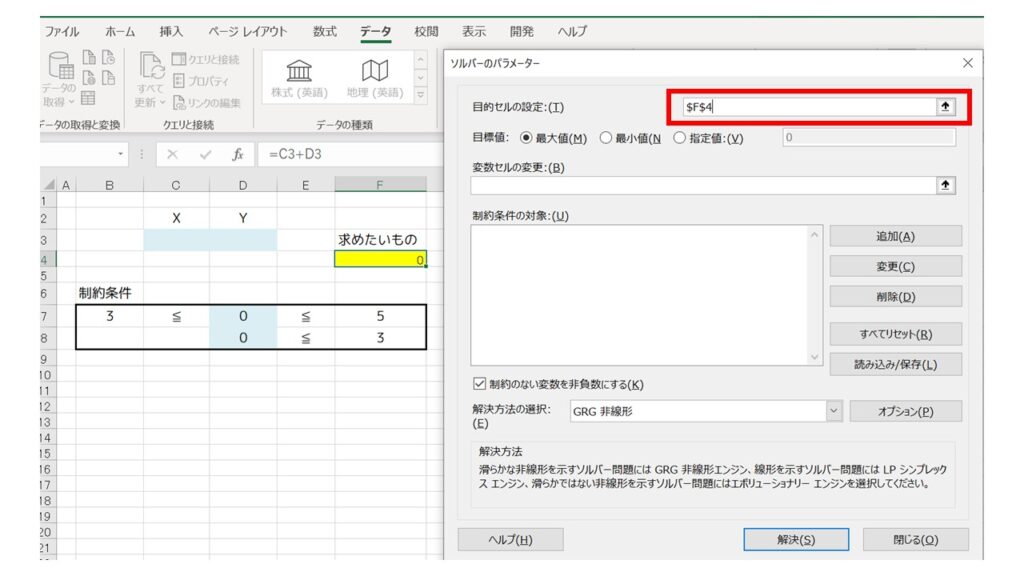
次に、目標値は『最大値』をクリックします。

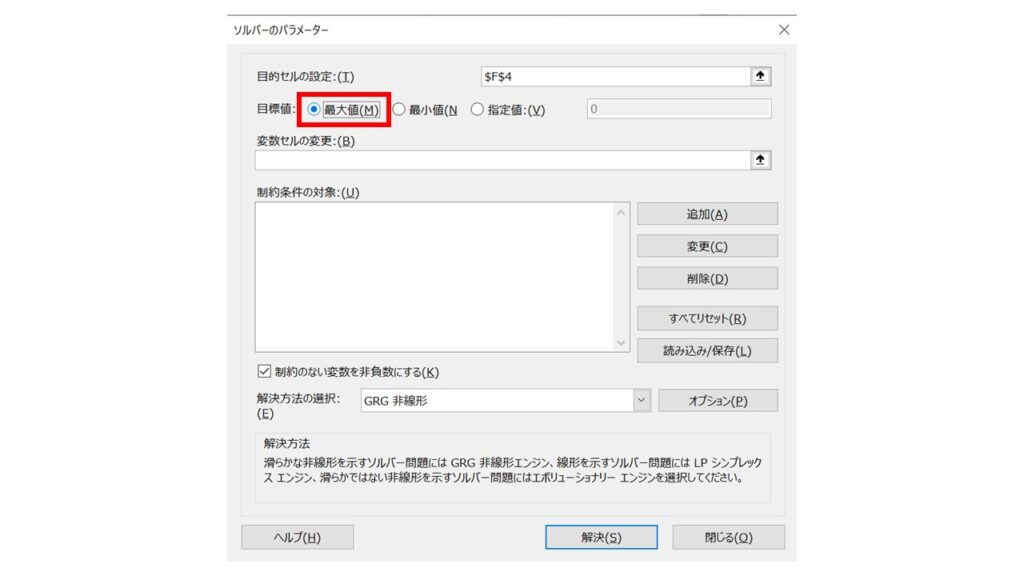
変数セルの変更欄に、今回の変数である XとY を指定します（C3セルとD3セル）

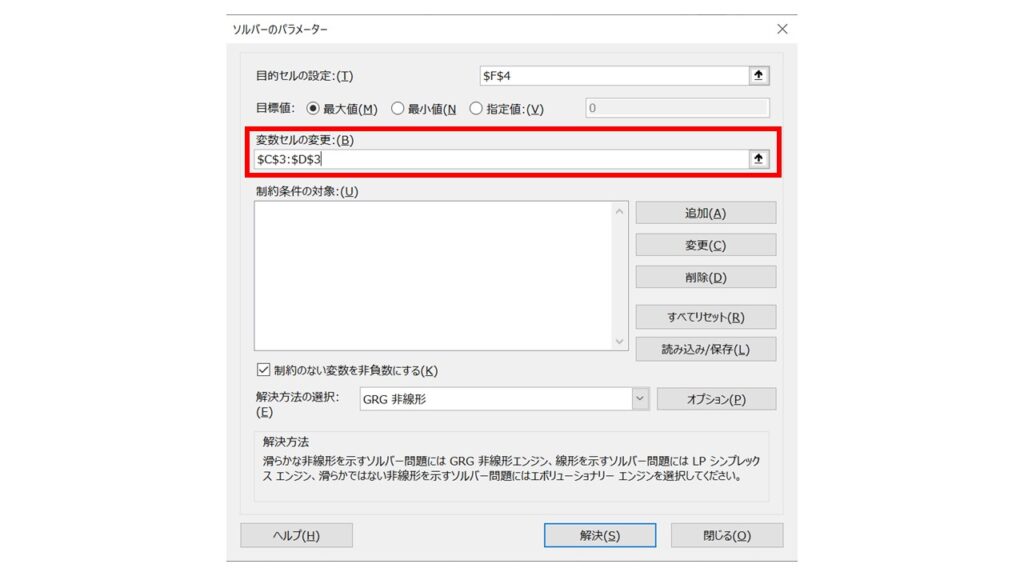
次に制約条件の対象を指定していきます。まずは『追加』ボタンをクリック。すると、『制約条件の追加』というウィンドウが開きます。

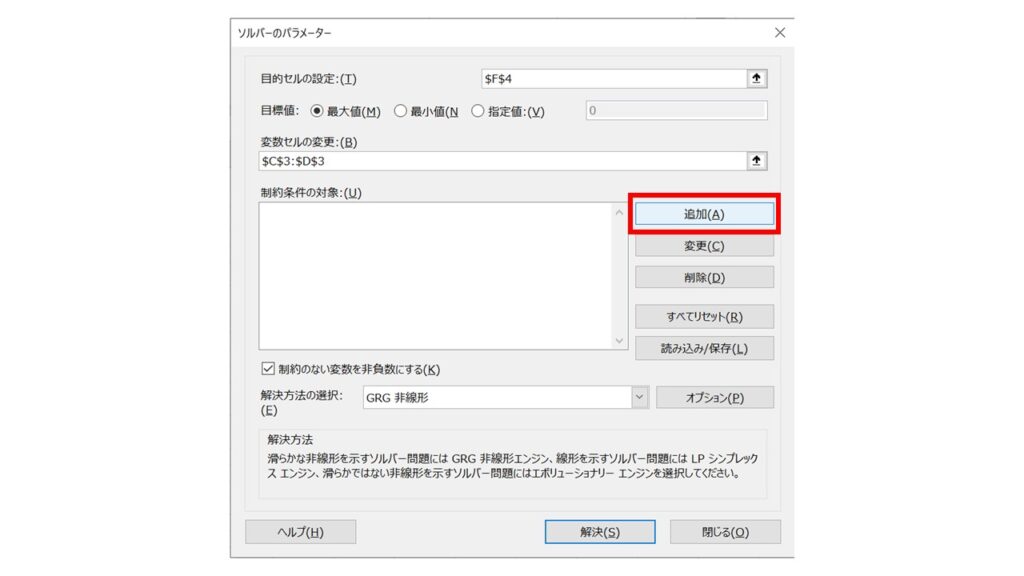
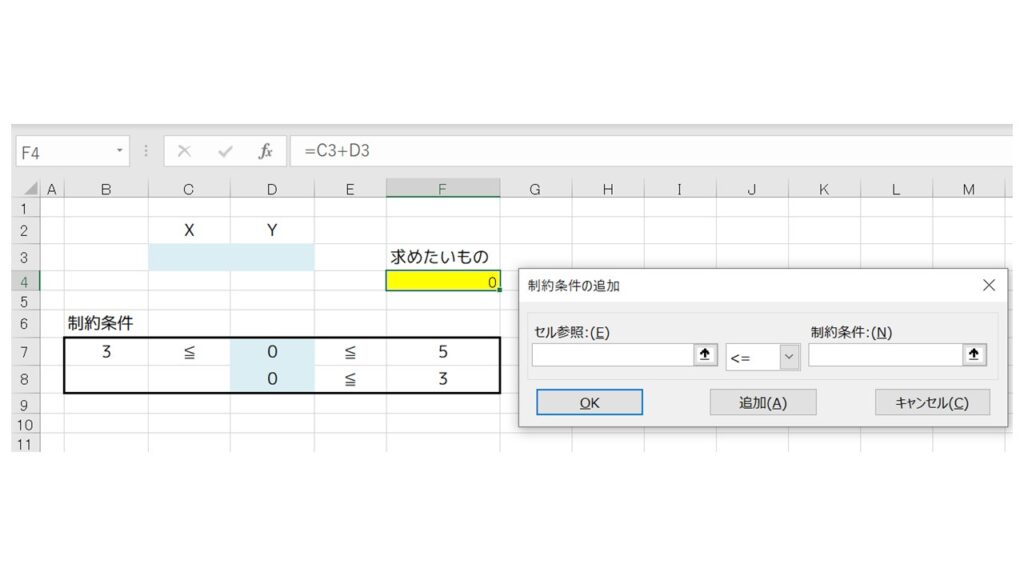
まずは、『セル参照』欄に X のセル（D7）を指定します。

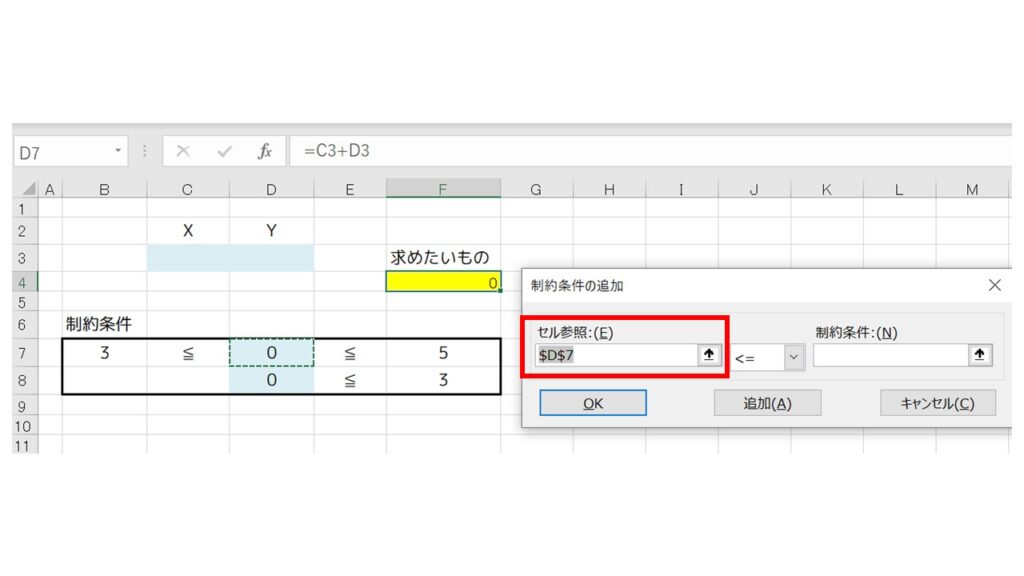
真ん中のドロップダウンは『≦』を選び、制約条件は『F7』セルを指定します。そして、『追加』をクリック。

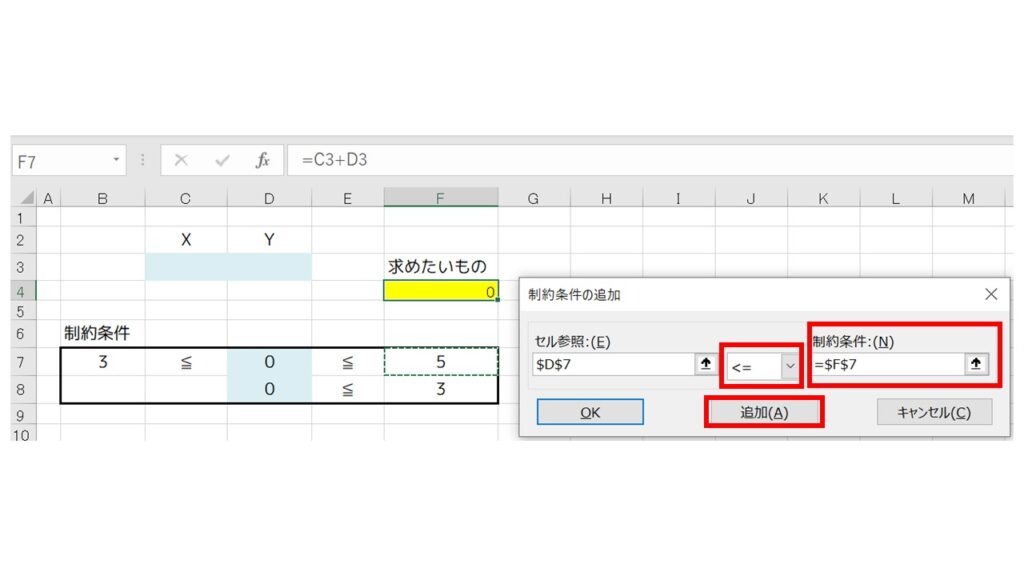
指定したセルが全てクリアになるので、『キャンセル』を押して『ソルバーのパラメーター』のウィンドウに戻ってみると、以下の制約条件が追加されているのが分かります。（$D$7 ≦ $F$7）

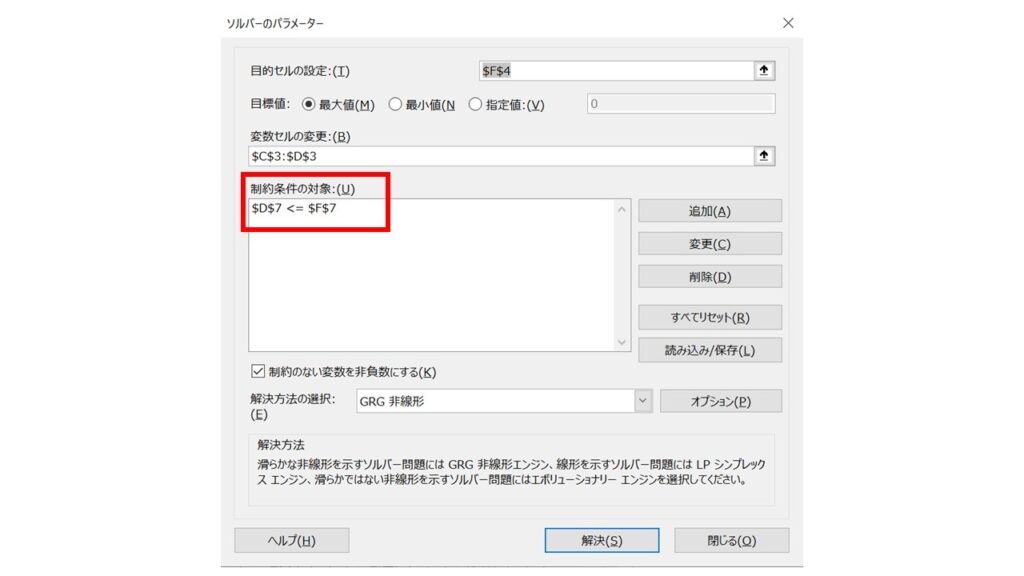
つまりこれで、『X≦5』の条件が追加されたことになります。同様に、『3≦X』の条件も追加してみましょう。『追加』ボタンを押します。

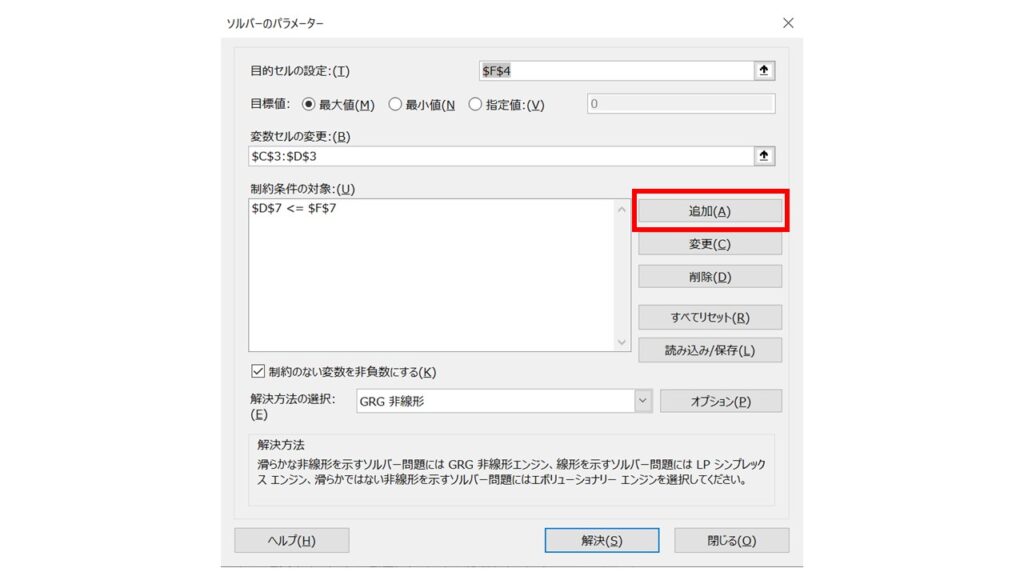
『制約条件の追加』ウィンドウが開くので、『セル参照』欄に X のセル（D7）を指定します。

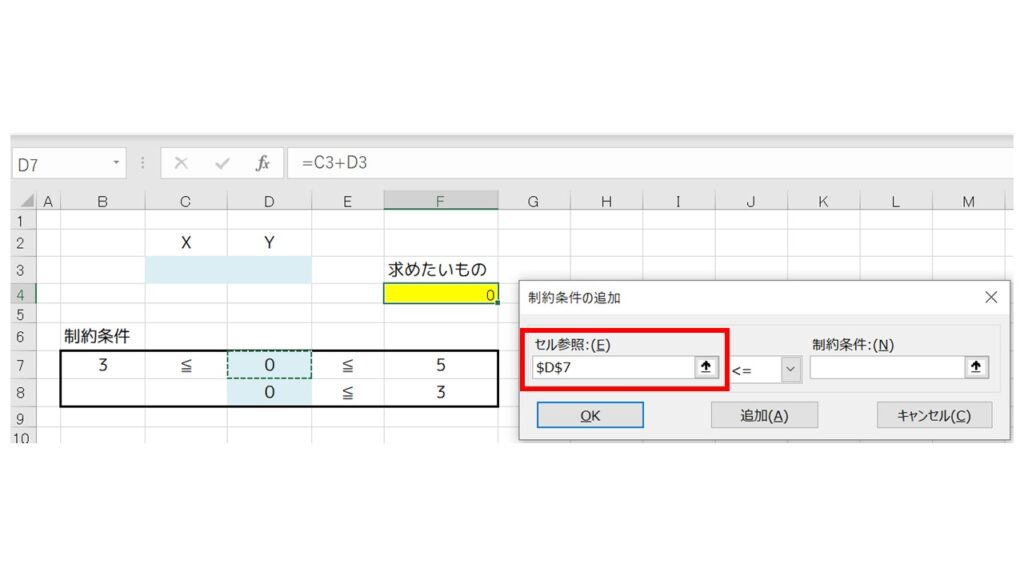
真ん中のドロップダウンは先ほどと逆の『≧』を選び、制約条件は『B7』セルを指定します。そして、『追加』をクリック。

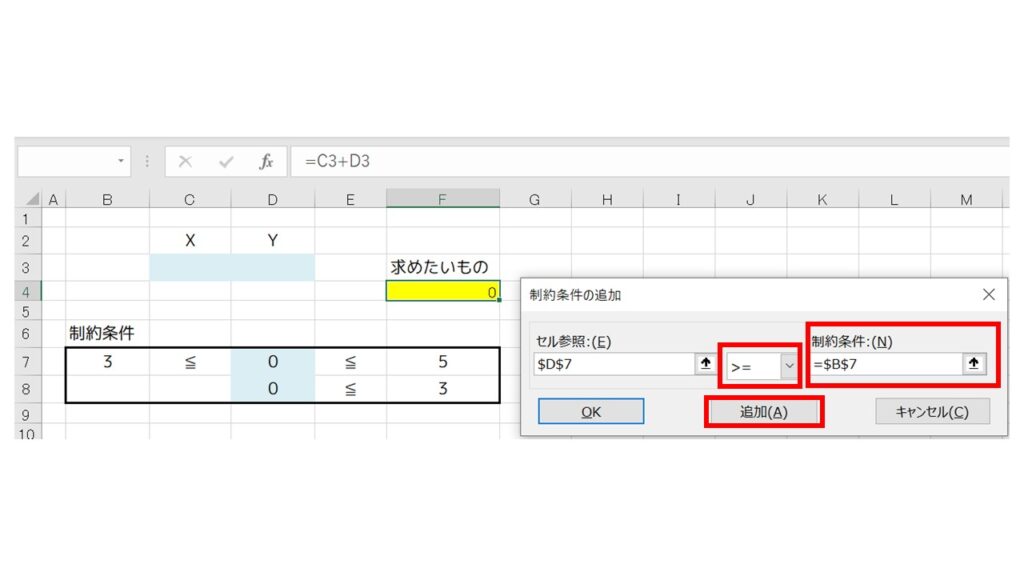
指定したセルが全てクリアになるので、『キャンセル』を押して『ソルバーのパラメーター』のウィンドウに戻って確認してみましょう。以下の制約条件が追加されているのが分かります。（$D$7 ≧ $B$7）

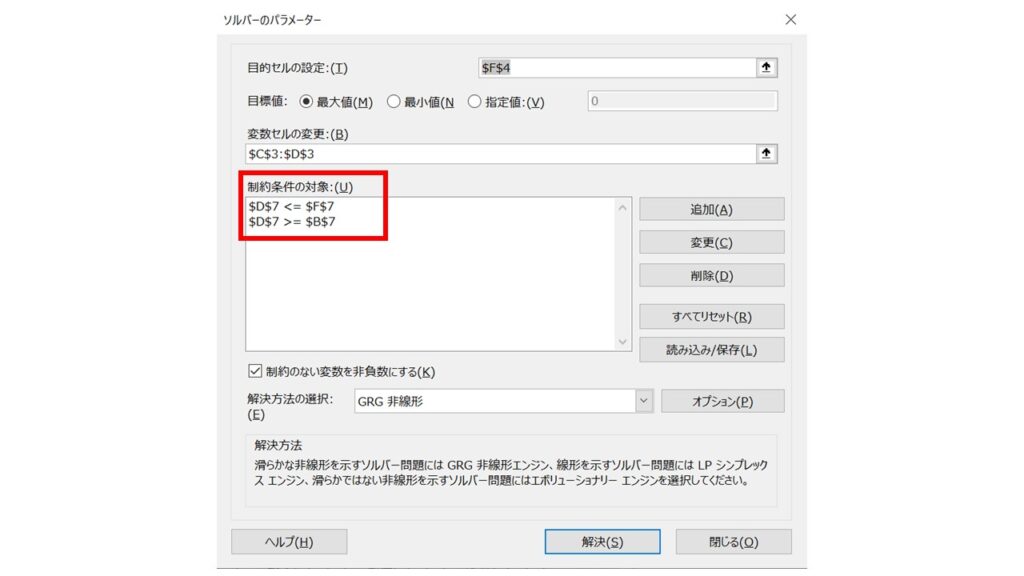
これで『3≦X≦5』の条件が完成しました。最後に、『Y≦3』の条件も追加してみましょう。もう手順はわかりますね。『追加』ボタンを押します。

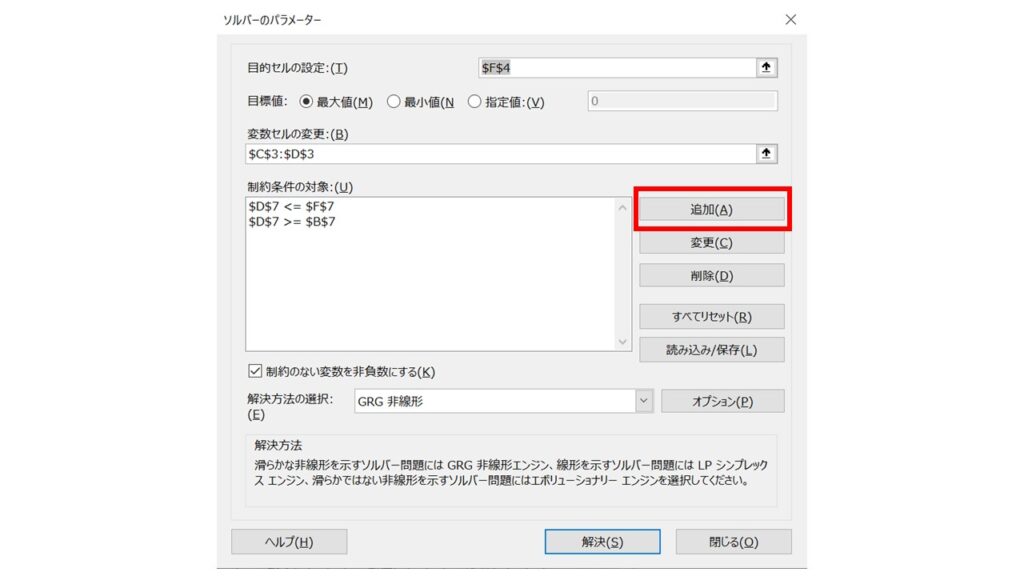
『制約条件の追加』ウィンドウが開くので、『セル参照』欄に Y のセル（D8）を指定します。

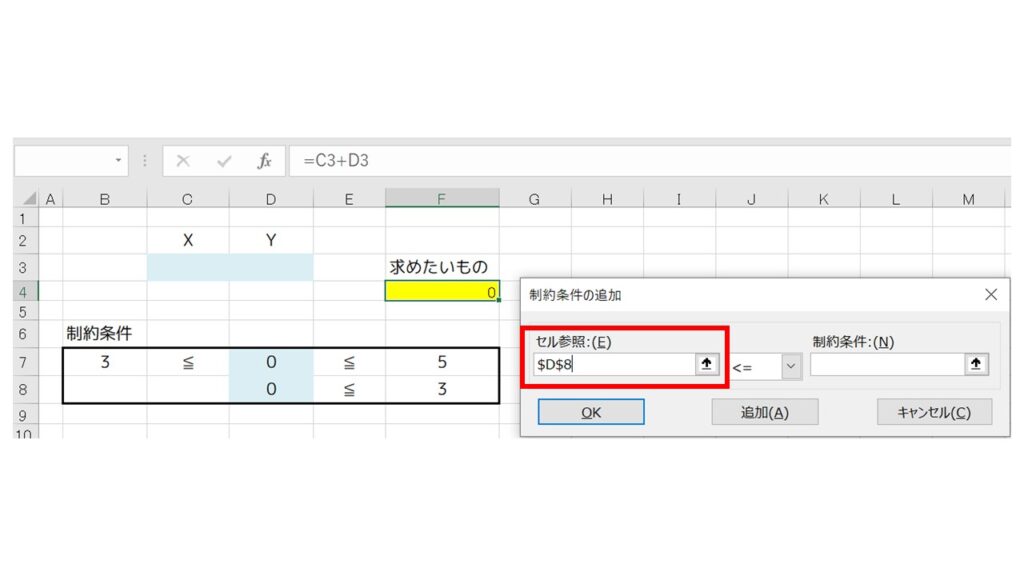
真ん中のドロップダウンは『≦』を選び、制約条件は『F8』セルを指定します。そして、『追加』をクリック。

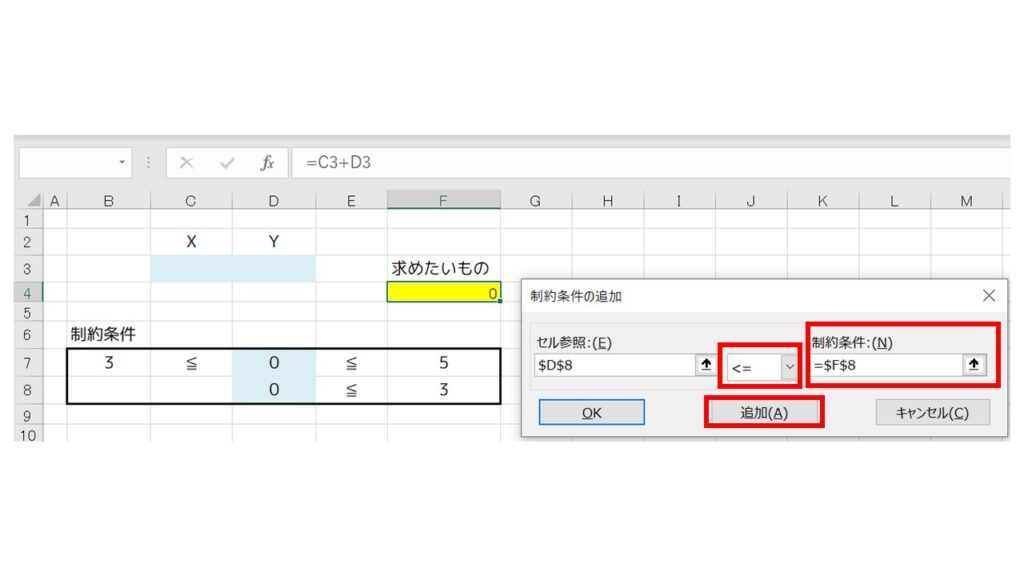
指定したセルが全てクリアになるので、『キャンセル』を押して『ソルバーのパラメーター』のウィンドウに戻って確認してみましょう。これで全ての制約条件が追加されました。

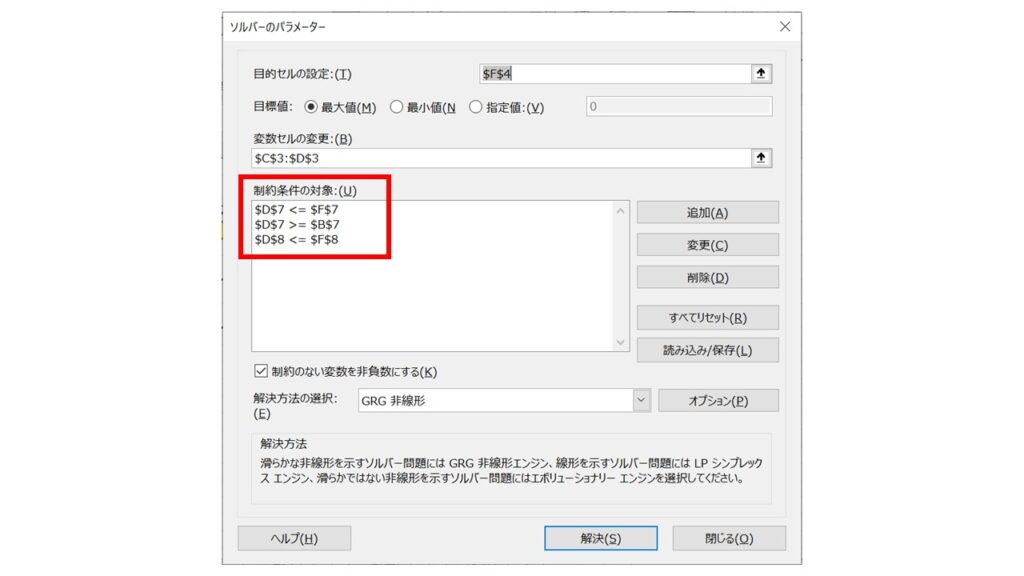
『制約のない変数を非負数にする』にチェックが入っていることを確認し、『解決方法の選択』欄は『シンプレックス LP』を選択します。最後に『解決』をクリックします！

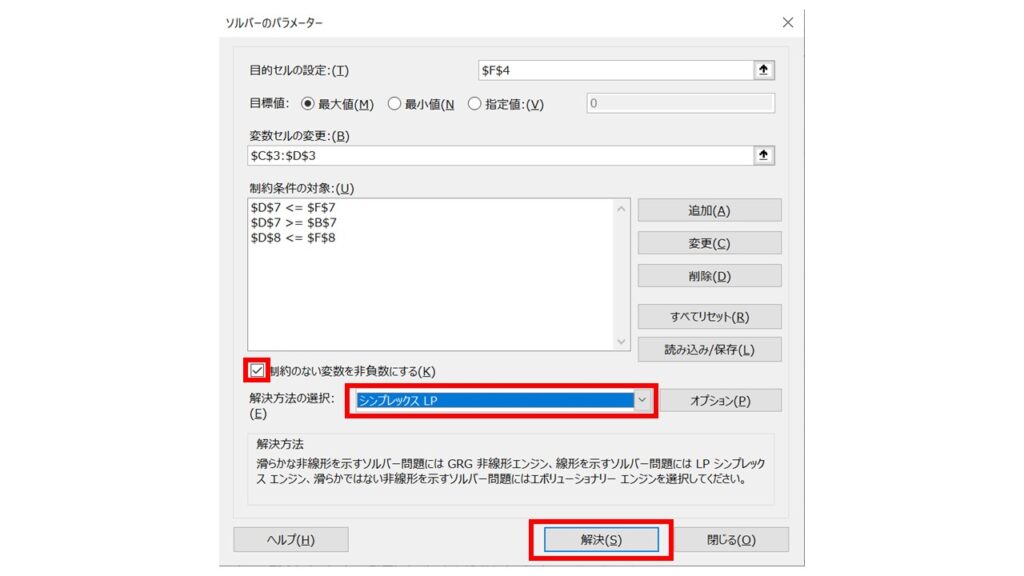
『ソルバーの結果』というウィンドウが表示され、指定した条件で自動計算がおこなわれました。『OK』をクリックします。

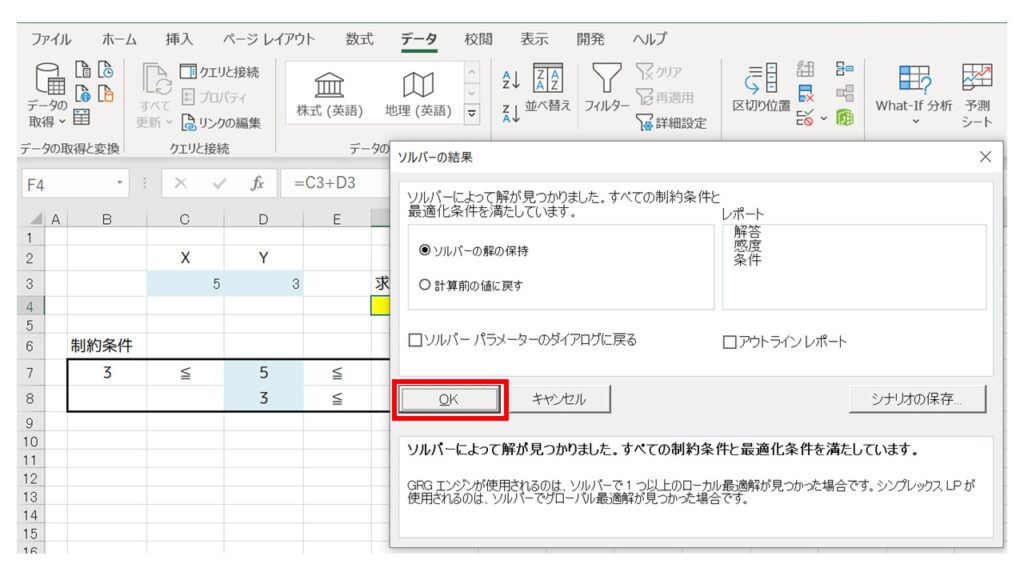
下図のように、変数XとYの値がそれぞれ 『X = 5、Y = 3』 と計算され、求めたいものである『X + Yの最大値』が『８』と計算されましたでしょうか？

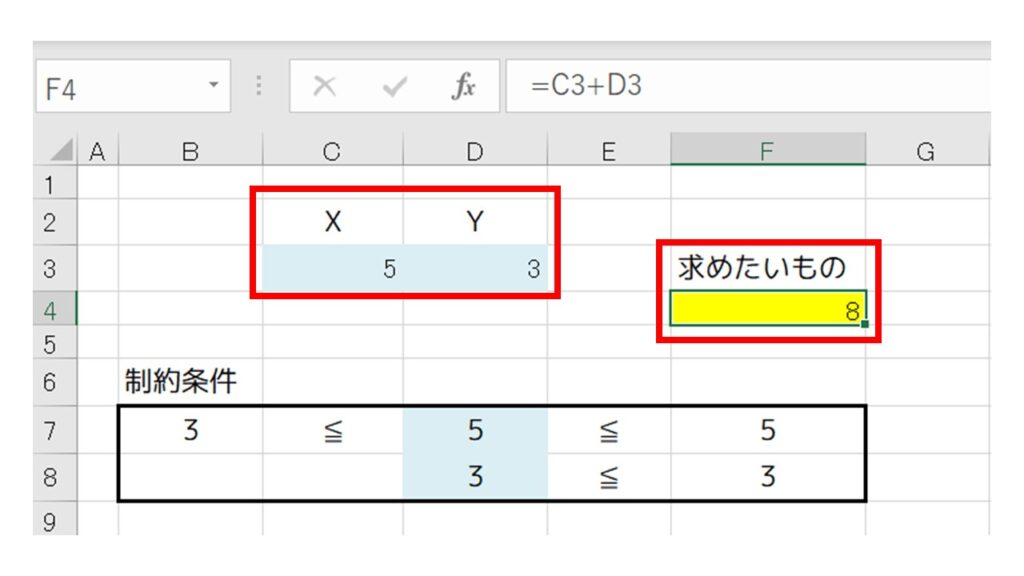
このように、ソルバーは『制約条件』を指定することで、『求めたいもの』の最適な値を自動計算させることができます。

それではソルバーの基本的な使い方が分かったところで例題です！
下記の『あおぞらカフェ』の例を用いて、材料や作業量などに限りがある時、どうやって利益を最大化するかをソルバーで計算してみましょう！

モジュール２：利益最大化

ここではカフェの経営者になったつもりで、『利益最大化』について考えてみましょう。

できること：ソルバーで利益最大化の計算をおこなう

このエクササイズでは、ソルバーを使ってカフェの利益を最大化する資源の配分方法を求めることができます。カフェでは、商品を作るために必要な資源（使える生地の量、および作業時間）が限られています。使える資源が限られている際の、利益最大化する資源の配分を計算することができます。

例題２

『あおぞらカフェ』では、フルーツタルトとスポンジケーキが人気商品です。それぞれの利益は以下になります。

次に、フルーツタルトおよびスポンジケーキ１個を作るのに必要な生地の量と作業時間（混ぜる時間・焼く時間）は以下の通りです。

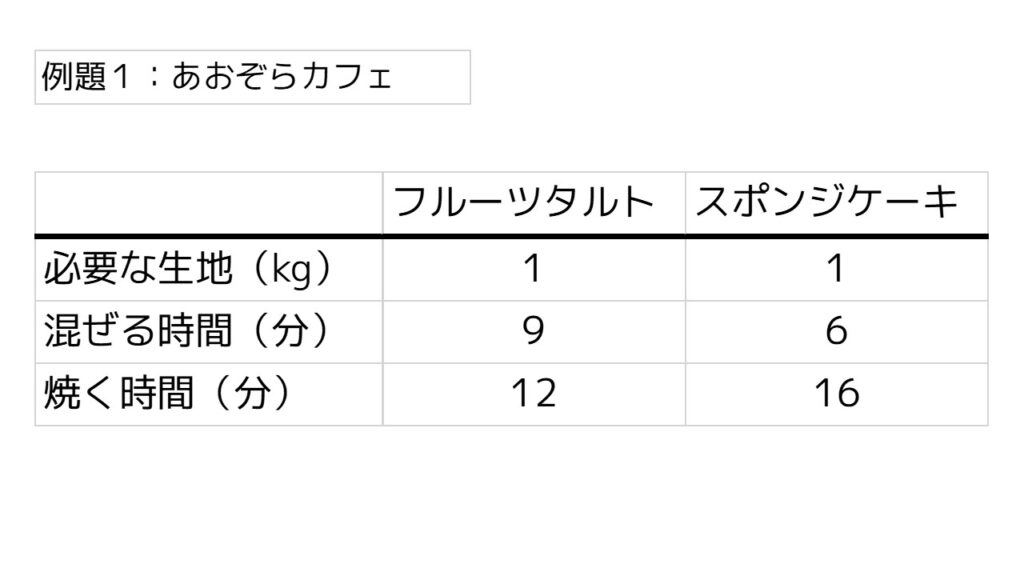
ただし、カフェで1週間に使える生地の量、および作業時間は限られています。

• 生地は200kgまで、混ぜる時間は1600分まで、焼く時間は2800分まで

フルーツタルトとスポンジケーキを何個ずつ作るのが最も利益が高いでしょうか？
（※カフェは毎日大盛況で、作ったタルトとケーキは全て売ることができるとします。）

解答

いかがでしょうか？ソルバー基本操作の項で説明した『３ステップ』を覚えていますか？

１つずつエクセルのソルバーで表現してみましょう。

ステップ１：『変化するもの（=変数）』を決める

例題１の場合の変数は何でしょうか？この場合は、フルーツタルトとスポンジケーキを作る個数が変数になります。よって、フルーツタルトを作る個数をX、スポンジケーキを作る個数をYとしてエクセルに定義しましょう。
下図のように、B5セルにフルーツタルトを作る個数（X）、C5セルにスポンジケーキを作る個数（Y）と定義します。

ステップ２：最終的に『求めたいもの』を決めて、計算式を入力する

次に、最終的に『求めたいもの』を決めます。この例題の場合は『カフェの利益を最大化』したいので、求めたいものは合計の利益になります。つまり、フルーツタルトを作る個数を（X）、スポンジケーキを作る個数を（Y）とすると、求めたいものは『350X ＋ 300Y』です。

これをエクセルで表すと下図のようになります。

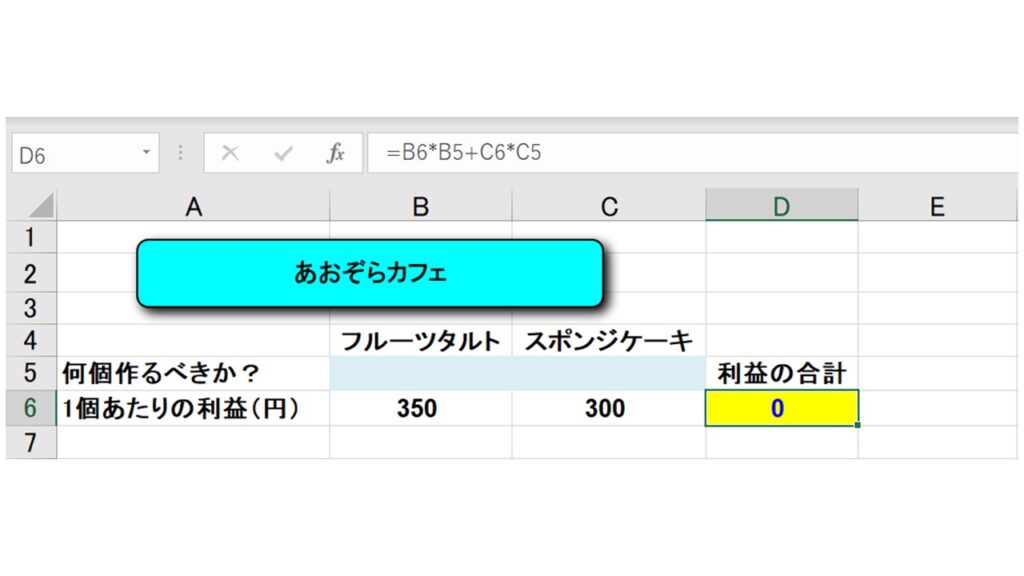
D6セルには数式 “=B6*B5+C6*C5” を入力して、利益の合計を入れます。

ステップ３：『制約条件』を入力する

最後に制約条件を入れましょう。この例題の制約条件は３つです。１週間に使える『生地の量』『混ぜる時間』『焼く時間』にそれぞれ制約があります。

例題の条件に戻ると、フルーツタルトとスポンジケーキ１個を作るのに必要な生地の量と作業時間（混ぜる時間・焼く時間）は以下の通りでした。

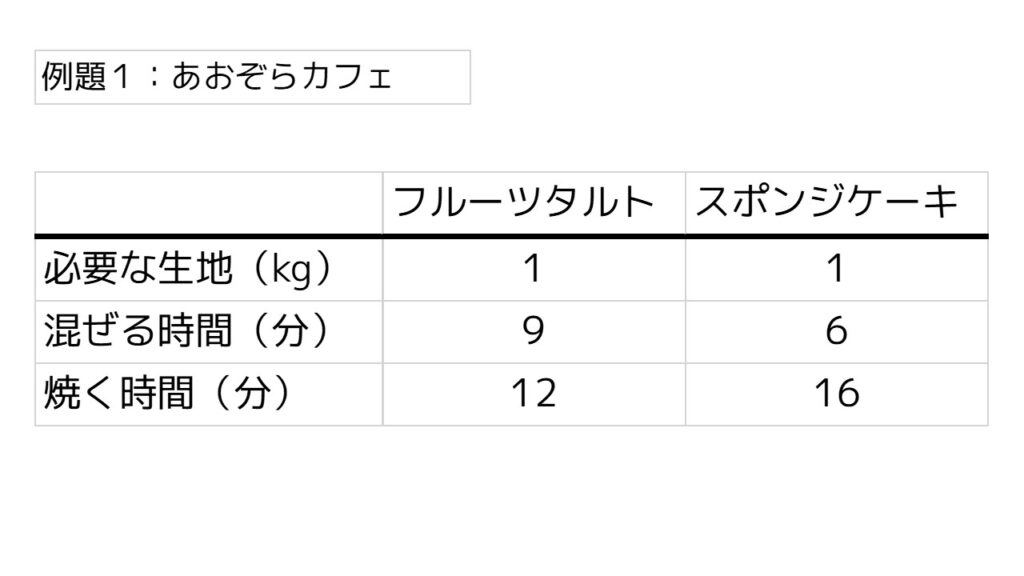
これをエクセルで表すとどのようになるでしょうか？下図を確認してください。

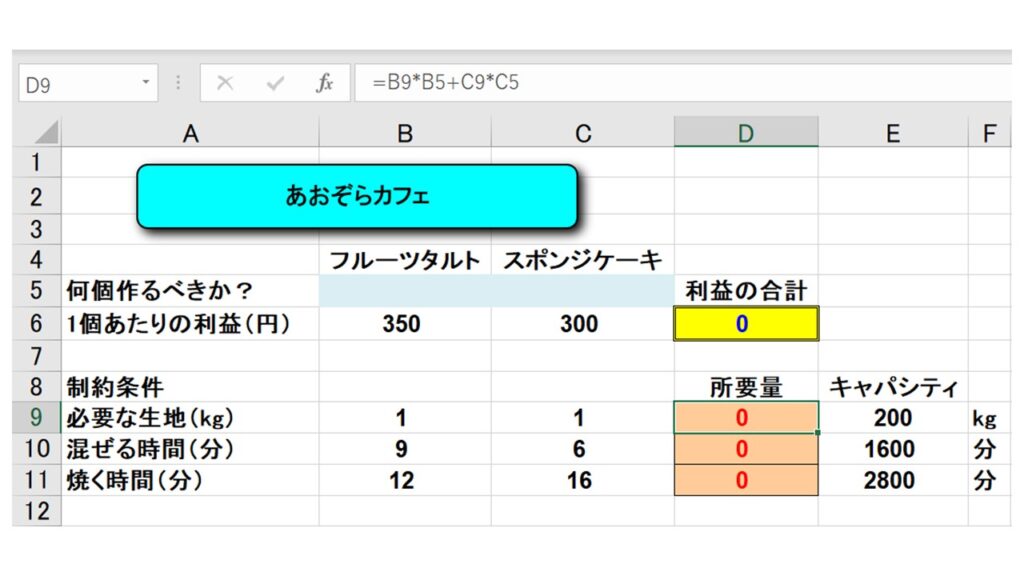
フルーツタルトを作る個数を B5（X）、スポンジケーキを作る個数を C5（Y）としたときに、

そして、それぞれ隣のセル（E9、E10、E11セル）にキャパシティ（=制約条件）を入力しました。

これで準備完了です。ソルバーを起動します。ソルバーのパラメーターは以下のように設定して『解決』ボタンを押しましょう。

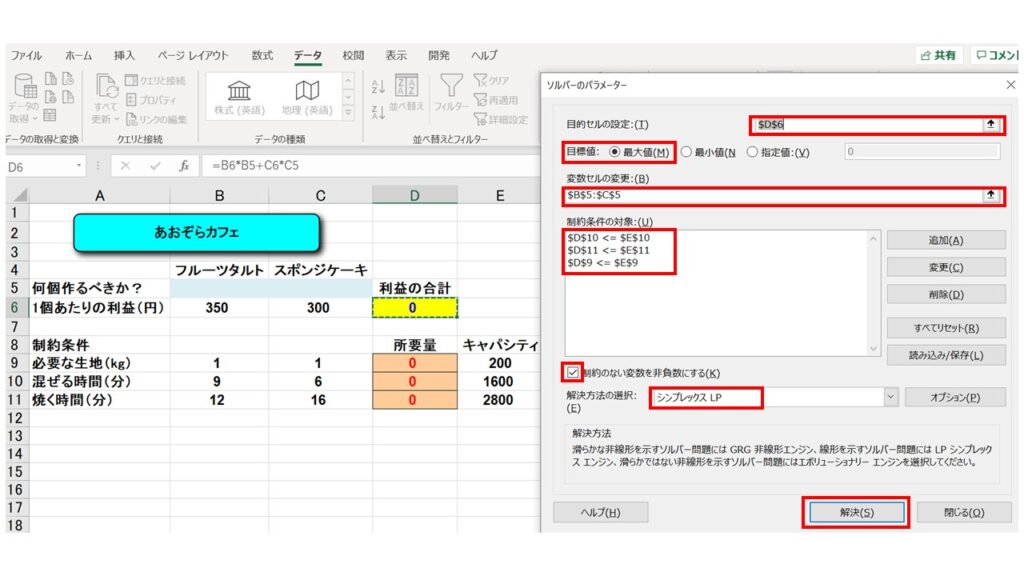
自動で計算がおこなわれ、以下のように『利益最大化』するために作るべきフルーツタルトとスポンジケーキの個数が算出されました！

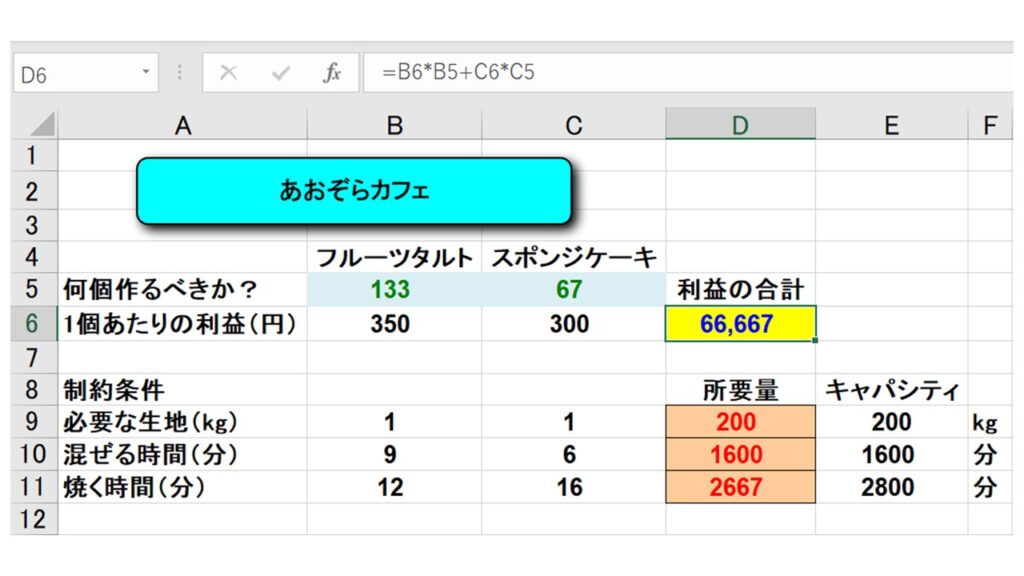
以上より、1週間でフルーツタルトを133個、スポンジケーキを67個作れば、あおぞらカフェは最大の利益66,667円を上げることができる、という結果になりました。

モジュール３：コスト最小化

次の例題では、電子部品を作っている企業が『いかにコストを最小化して受注した注文を100%満たせるか？』をソルバーを使って計算します。

できること： 作るべきか、買うべきか？（Make or Buy?）を意思決定する

この例題では、企業内でよく検討される『自分たちで作るべきか？それとも外部にアウトソース（委託）すべきか？』という『Make or Buy?』の意思決定をするためのソルバー計算を学ぶことができます。

例題３

あなたは電子部品を作る会社『（株）なつぐも電子工業』を経営しています。なつぐも電子工業では、３つのモデルの電子部品を作っています。（電子部品１、２、３）

今月、得意先から電子部品１、２、３それぞれについて下記の数の注文を受注しました。納期は１ヶ月です。自社の工場のキャパシティを考えながら『製造コストを最小化』して、注文数を100%満たすために最適な生産数量を計算してください。

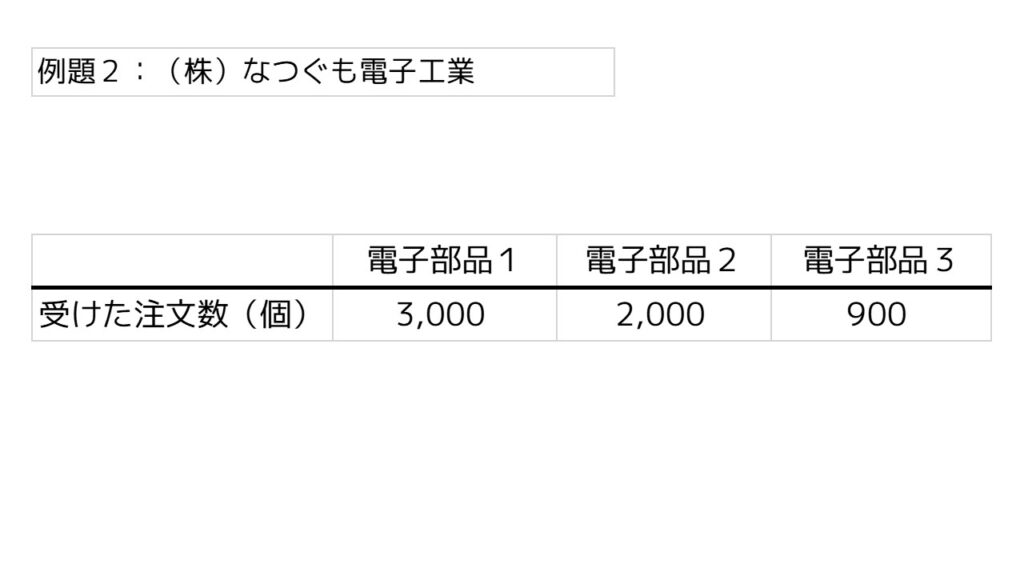
それぞれの電子部品１個を自社の工場で製造するのに必要な時間（労働力）は以下の通りです。

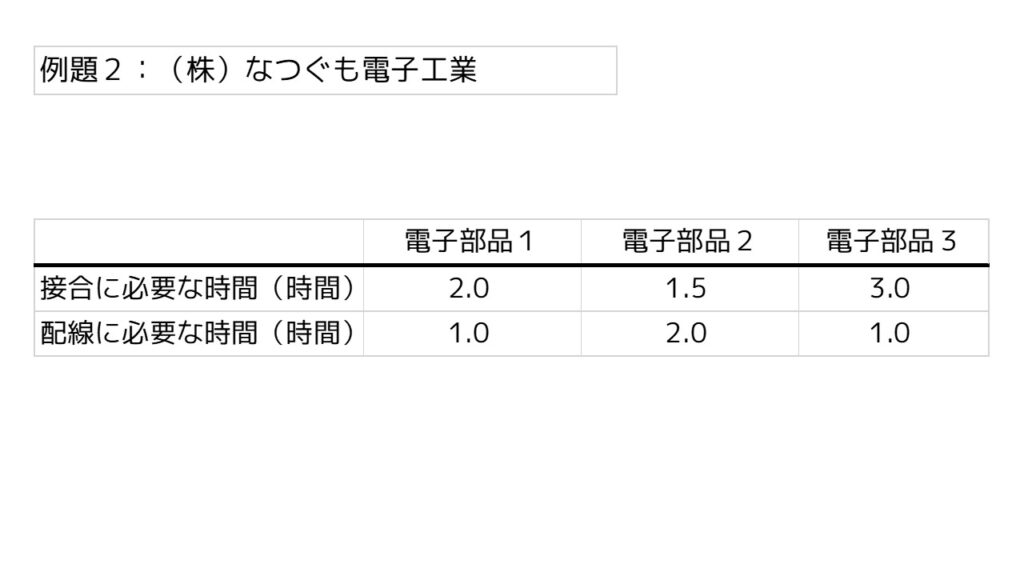
ただし、自社の工場で1ヶ月に使える労働力（キャパシティ）は限られています。

電子部品は自社の工場で自作することもできますが、アウトソーシング（委託）して調達することもできます。電子部品１個あたり、自作にかかるコストとアウトソーシングして調達するコストは以下の通りです。

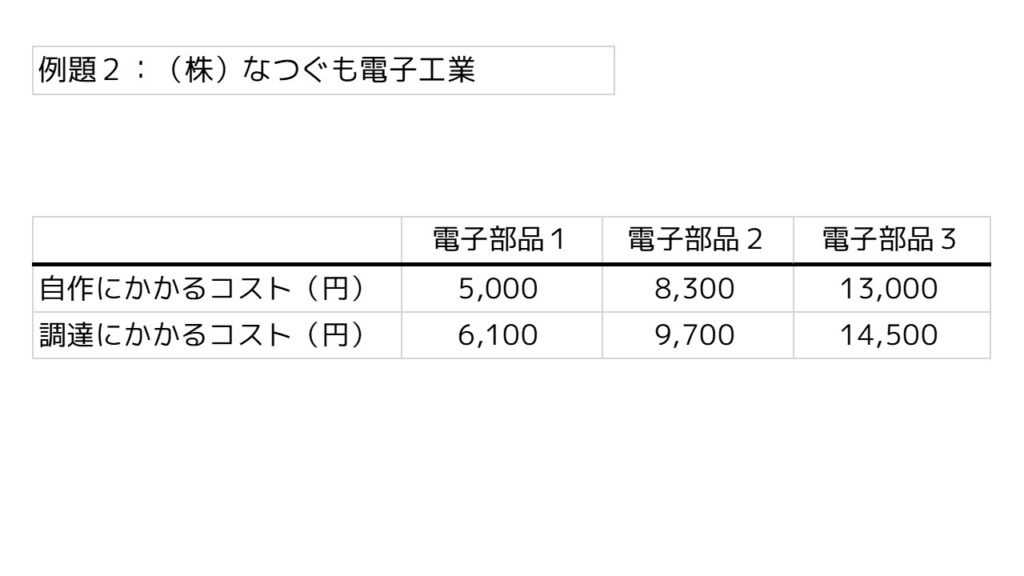
電子部品１、２、３をそれぞれ何個自作し、何個アウトソーシングすれば製造コストを最小化できるでしょうか？ソルバーで計算してください。

解答

いかがでしょうか？今回は例題１の応用になります。

ヒントは例題２の場合、 ”変数” は６つになります。（電子部品１、２、３を自作する数をA、B、Cとして、アウトソーシングする数を D、E、Fとすると合計６つの変数になります。）

それでは今回も『３ステップ』で解いていきましょう！

ステップ１：『変化するもの（=変数）』を決める

今回の場合は電子部品１、２、３を自作する数をA、B、Cとして、アウトソーシングする数を D、E、Fとすると、変数は合計６つになります。

よって以下のようにB6～D6セルに電子部品１、２、３を自作する数を定義します。同様にB7～D7セルにアウトソーシングして調達する数を定義します。

ステップ２：最終的に『求めたいもの』を決めて、計算式を入力する

次に、最終的に『求めたいもの』を決めます。例題2の場合は『製造コストを最小化』するための最適な生産数量を計算したいので、求めたいものは『製造コストの合計』になります。つまり、電子部品１、２、３を自作する数をA、B、C、アウトソーシングする数を D、E、Fとすると、求めたいものは『5000×A ＋ 8300×B + 13000×C + 6100×D ＋ 9700×E + 14500×F』です。

これをエクセルで表すと下図のようになります。

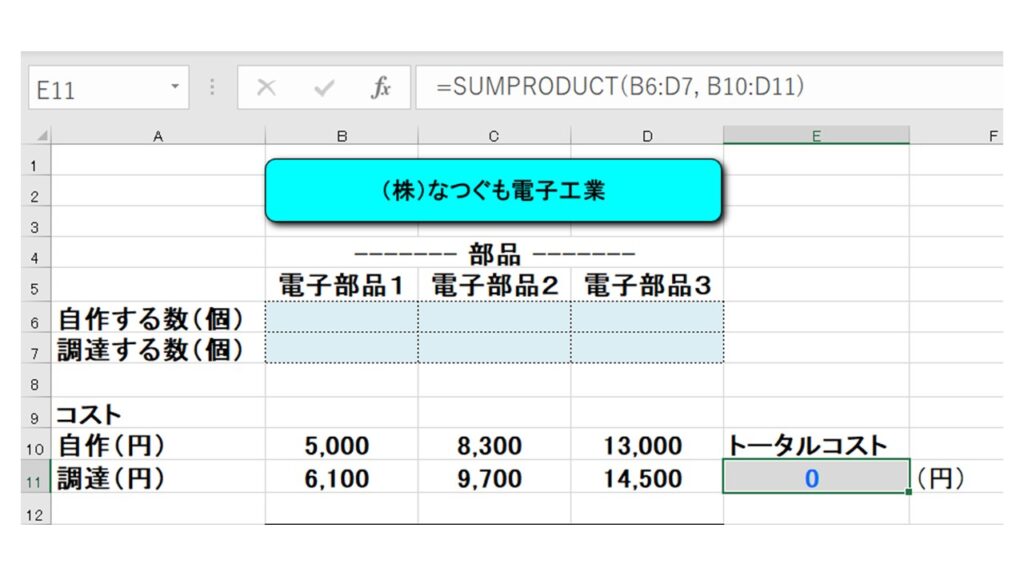
E11セルには『製造コストの合計』を求める計算式 “=B6*B10 + C6*C10 + D6*D10 + B7*B11 + C7*C11 + D7*D11” を入力します。

また、このときに便利な関数があります。 ”SUMPRODUCT” です。E11セルに “=SUMPRODUCT(B6:D7, B10:D11)” と入力するだけで、上記の計算式と同じ意味になりますので是非覚えておきましょう！

ステップ３：『制約条件』を入力する

最後に制約条件を入れましょう。この例題の制約条件は２つです。自社の工場で1ヶ月に使える労働力、つまり『接合』『配線』の時間にそれぞれ制約があります。接合時間は10,000時間まで、配線時間は5,000時間までです。

例題の条件に戻ると、電子部品１～３をそれぞれ自作するのに必要な作業時間（接合時間と配線時間）は以下の通りでした。

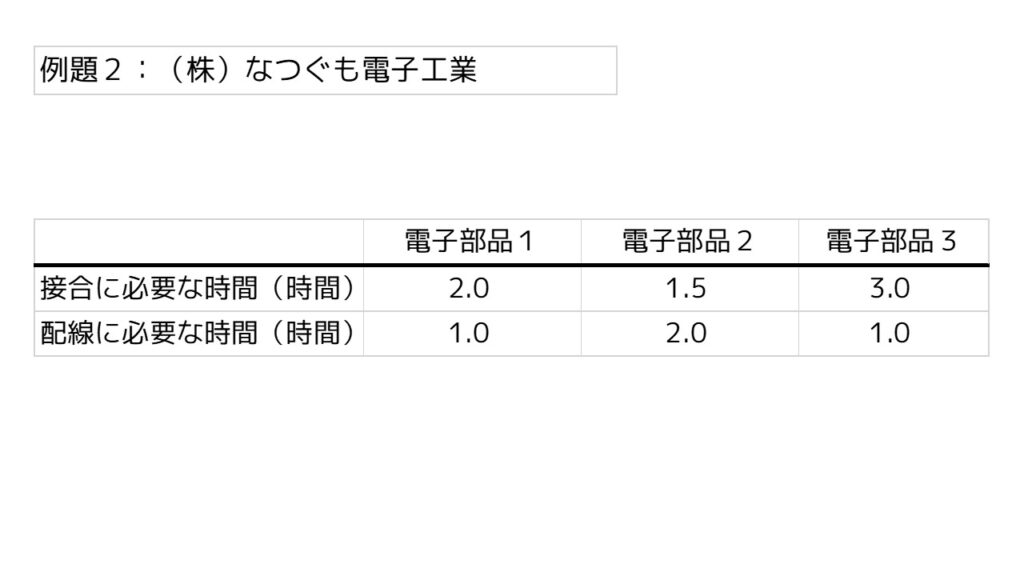
これをエクセルで表すとどのようになるでしょうか？下図を確認してください。

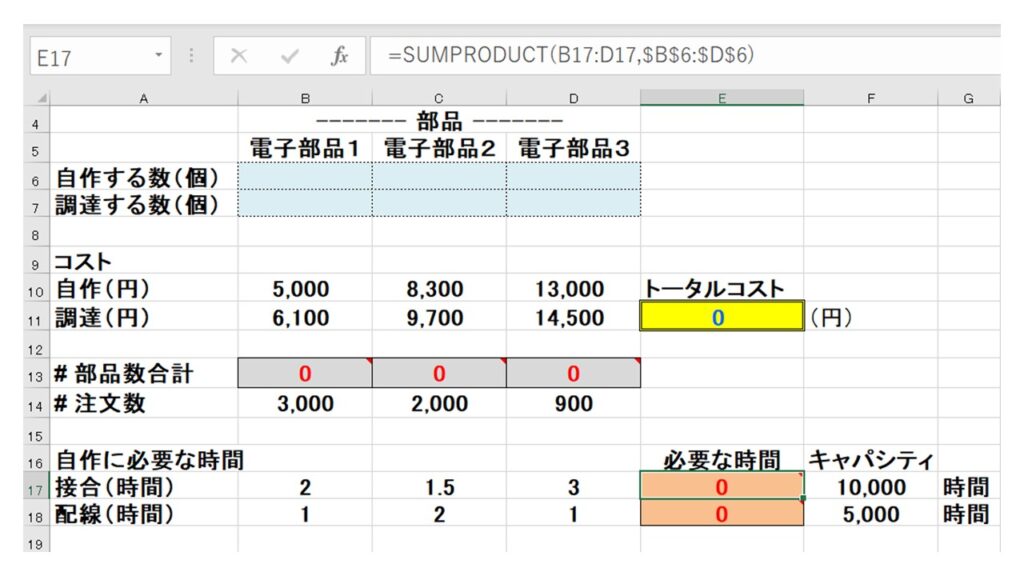
早速、先ほど学んだ “SUMPRODUCT” 関数を使いました。

そして、それぞれ隣のセル（F17、F18）にキャパシティ（=制約条件）を入力しました。

最後に、自作もしくは調達した部品数の合計が注文数を満たさないといけないので、下記の計算式を入力しました。

そして、それぞれの受注数を隣のセル（B14、C14、D14）に入力しました。

これで準備完了です。ソルバーを起動します。ソルバーのパラメーターは以下のように設定して『解決』ボタンを押しましょう。今度は『コストを最小化』したいので、目標値は『最小値』にチェックすることを間違えないようにしましょう。

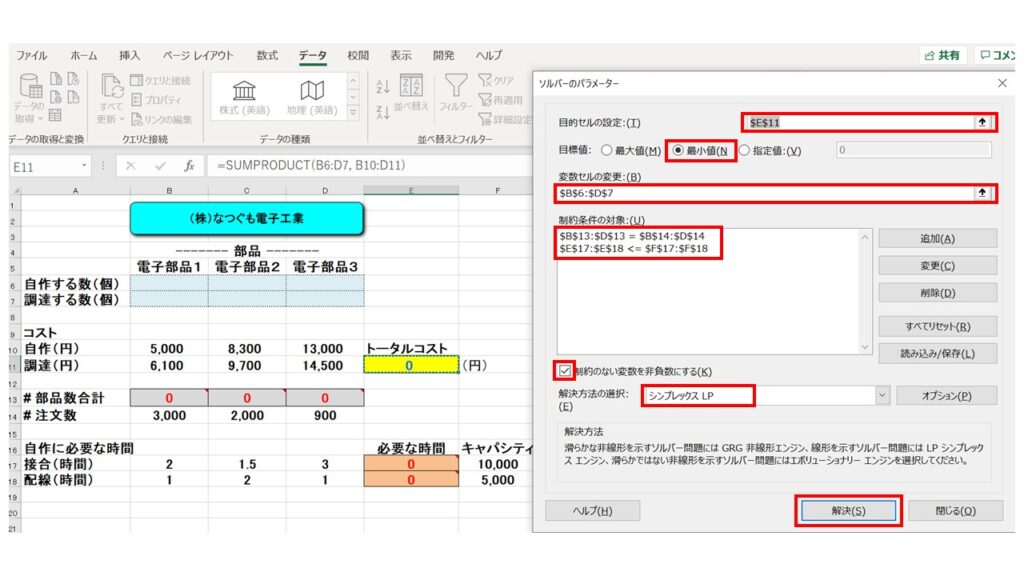
自動で計算がおこなわれ、以下のように『製造コストを最小化』するために自作するべき部品の数と、調達すべき部品の数が算出されました！

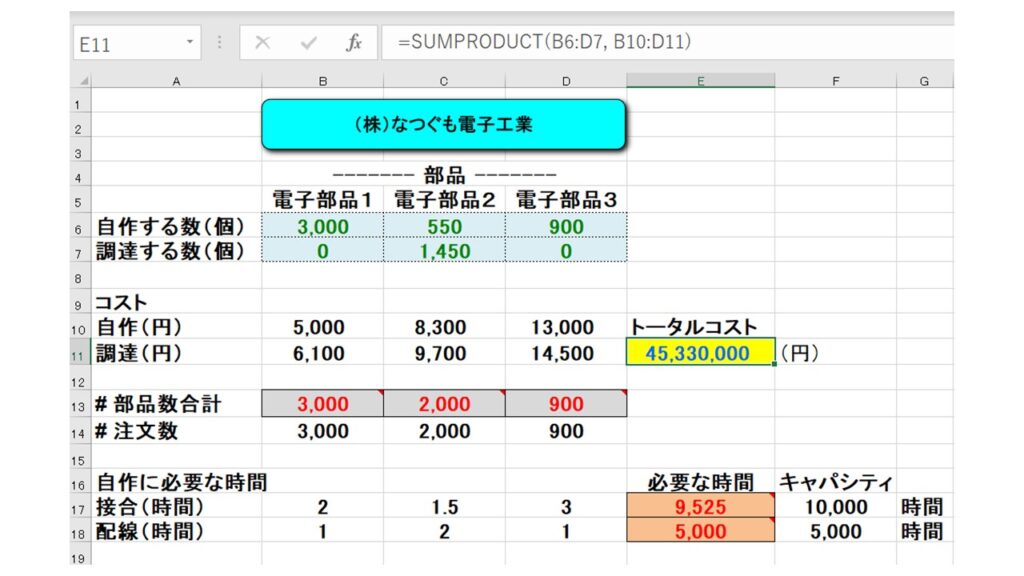
以上より、１ヶ月で自作すべき電子部品１は3,000個、電子部品２は550個、電子部品３は900個、調達すべき電子部品２は1,450個ということが分かりました。この通りに製造すれば、なつぐも電子工業は『製造コストを最小化』して、注文数を100%満たすことができる、という結果になりました。

モジュール４：感度レポートの考え方

次の例題では、ソルバーで計算をした際に得られる有用なレポート機能について学びます。具体的には、『解答レポート』と『感度レポート』の内容を解説します。

できること： ソルバーの感度レポートを理解する（潜在価格と許容範囲）

この例題では、例題１で学んだ『利益最大化』の考え方を使いながら、ソルバーのレポートで最も有益な情報である『感度レポート』の解釈方法と、『潜在価格』『許容範囲』の考え方を理解することができます。これを理解すれば、『どうすれば利益をさらに増やすことができるか』という経営の意思決定に関わる重要な情報を読み取ることができるようになります。

例題４

『青山ベーカリー』では、クロワッサンとフレンチトーストが人気商品です。それぞれのパン1個あたりの利益は以下になります。

青山ベーカリーでは、1日に売れるクロワッサンの個数（需要）は90個、フレンチトーストの個数（需要）60個になります。

次に、クロワッサンおよびフレンチトースト１個を作るのに必要な作業時間（混ぜる時間・焼く時間）は以下の通りです。

ただし、ベーカリーで1日に使える作業時間は限られています。

• 一日のうち、混ぜる時間は465分まで、焼く時間は420分まで

クロワッサンとフレンチトーストを何個ずつ作るのが最も利益が高いでしょうか？

解答

いかがでしょうか？例題１の類似問題になります。同様に３ステップで解いていきましょう。

ステップ１：『変化するもの（=変数）』を決める

例題１同様に、最初に『変数』を決めます。この場合は、クロワッサンとフレンチトーストを作る個数が変数になりますね。よって、クロワッサンを作る個数をX、フレンチトーストを作る個数をYとしてエクセルに定義しましょう。
下図のように、B5セルにクロワッサンを作る個数（X）、C5セルにフレンチトーストを作る個数（Y）と定義します。

ステップ２：最終的に『求めたいもの』を決めて、計算式を入力する

次に、最終的に『求めたいもの』を決めます。この例題の場合は『ベーカリーの利益を最大化』したいので、求めたいものは合計の利益になります。つまり、クロワッサンを作る個数を（X）、フレンチトーストを作る個数を（Y）とすると、求めたいものは『50X ＋ 60Y』です。

これをエクセルで表すと下図のようになります。

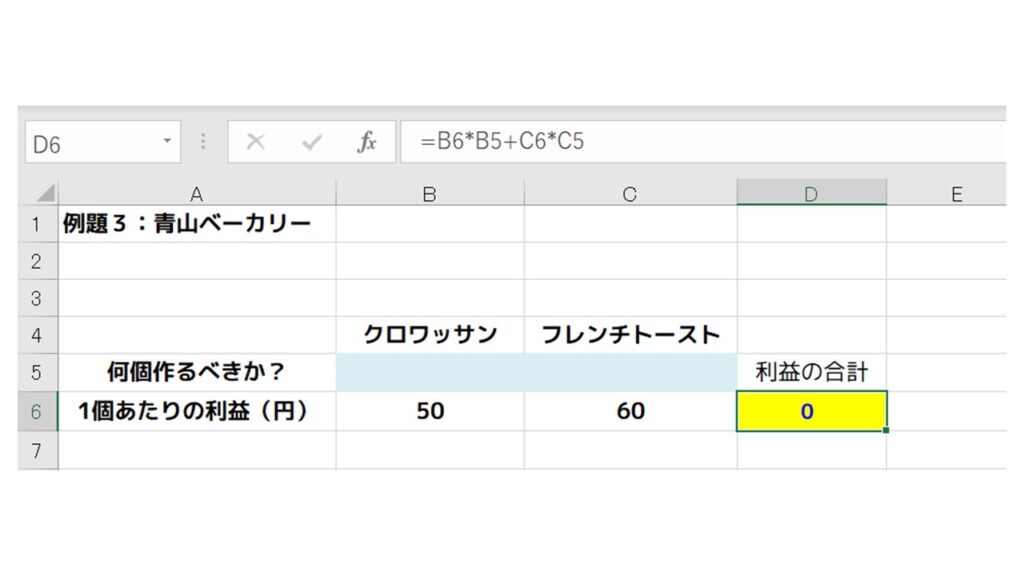
D6セルには数式 “=B6*B5+C6*C5” を入力して、利益の合計を入れます。

ステップ３：『制約条件』を入力する

最後に制約条件を入れましょう。この例題の制約条件は大きく分けて２つあります。１つは１日に売れるパンの個数の制約。もう１つは１日に使える作業時間、つまり『混ぜる時間』『焼く時間』にそれぞれ制約があります。

例題の条件に戻ると、クロワッサンとフレンチトースト１個を作るのに必要な作業時間（混ぜる時間・焼く時間）は以下の通りでした。

これをエクセルで表すとどのようになるでしょうか？下図を確認してください。

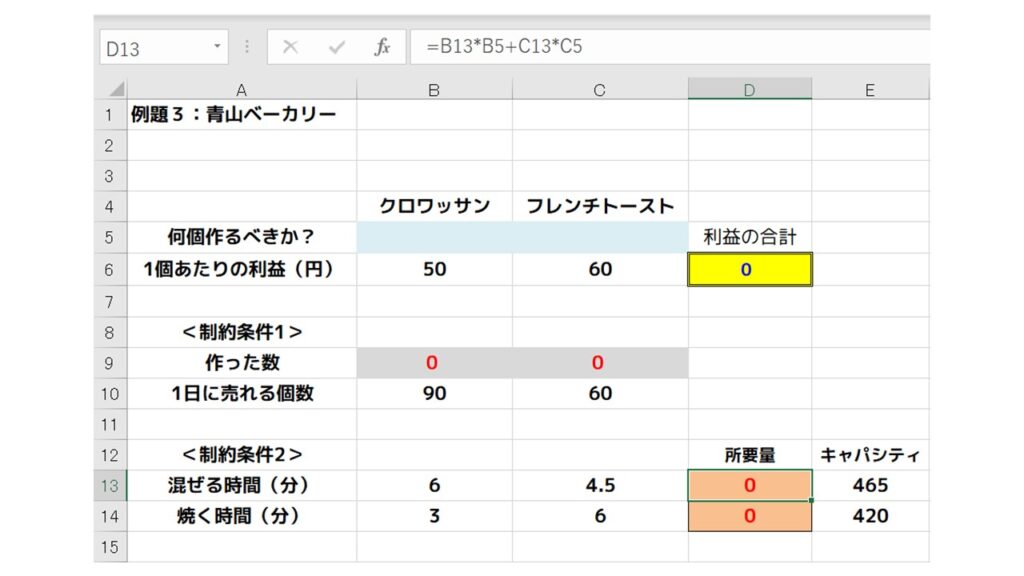
クロワッサンを作る個数を（X）、フレンチトーストを作る個数を（Y）としたときに、

〈制約条件1〉
作るべきクロワッサンとフレンチトーストの個数は、1日に売れる数（需要）以下でなければいけない

〈制約条件2〉
1日の混ぜる時間と焼く時間の合計は、それぞれ465分、420分以下でなければならない

これで準備完了です。ソルバーを起動します。ソルバーのパラメーターは以下のように設定して『解決』ボタンを押しましょう。

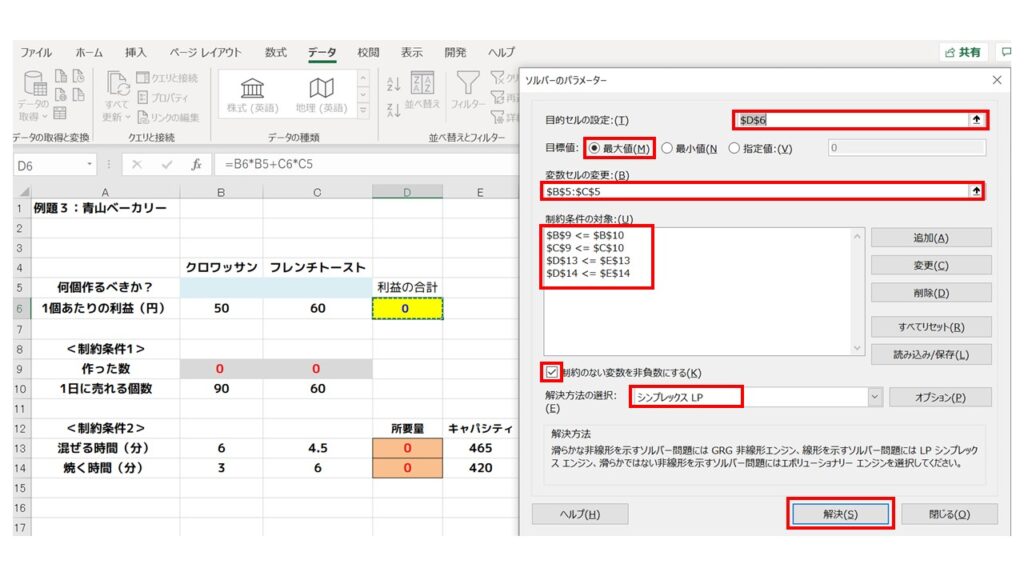
解決ボタンを押すと、『ソルバーの結果』ウィンドウが開くので、ここでレポートランにある『解答』『感度』『条件』レポートを選択して、『OK』をクリックしてください。

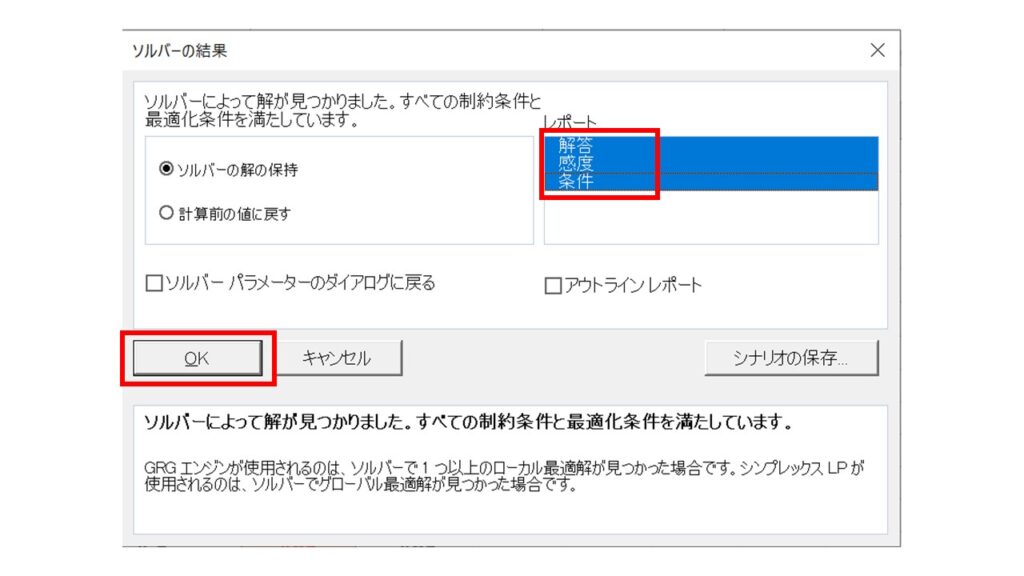
すると、同じエクセルファイルの別シートに『解答レポート』『感度レポート』『条件レポート』が自動で作成されます。

同時にソルバー計算が自動でおこなわれ、以下のように『利益最大化』するために作るべきクロワッサンとフレンチトーストの個数が算出されました！

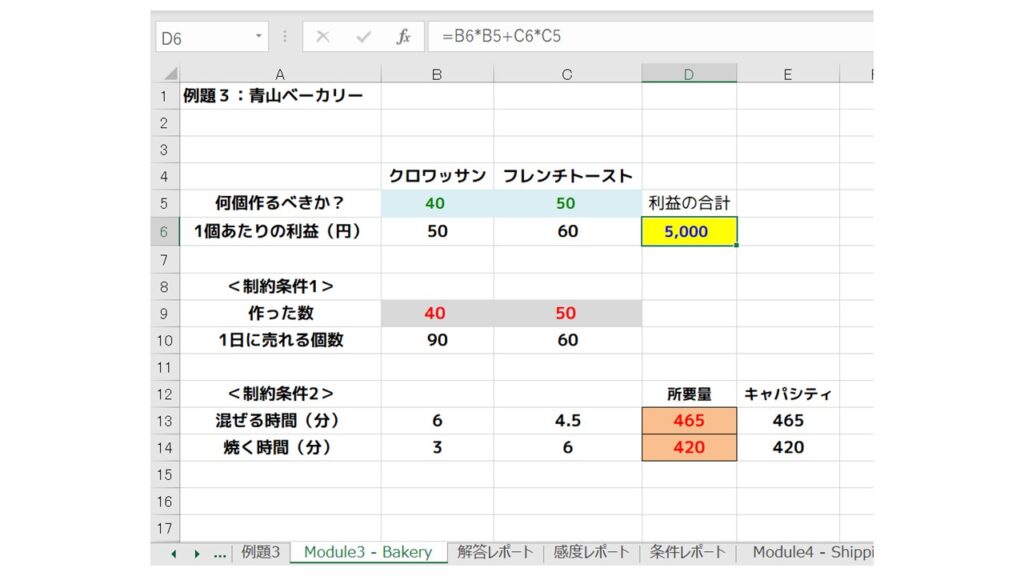
以上より、1日あたりクロワッサンを40個、フレンチトーストを50個作れば、青山ベーカリーは最大の利益5,000円を上げることができる、という結果になりました。

ソルバー結果をグラフで解釈する

ここまでソルバーの基本に沿って３ステップで解いてきました。レポートの解説に進む前に、今回の結果をグラフで視覚的に理解してみましょう。

制約条件をグラフで表す

以下のように、横軸（X）にクロワッサンを作る個数、縦軸（Y）にフレンチトーストを作る個数を示すグラフを作成すると、制約条件はどのように表せるでしょうか？

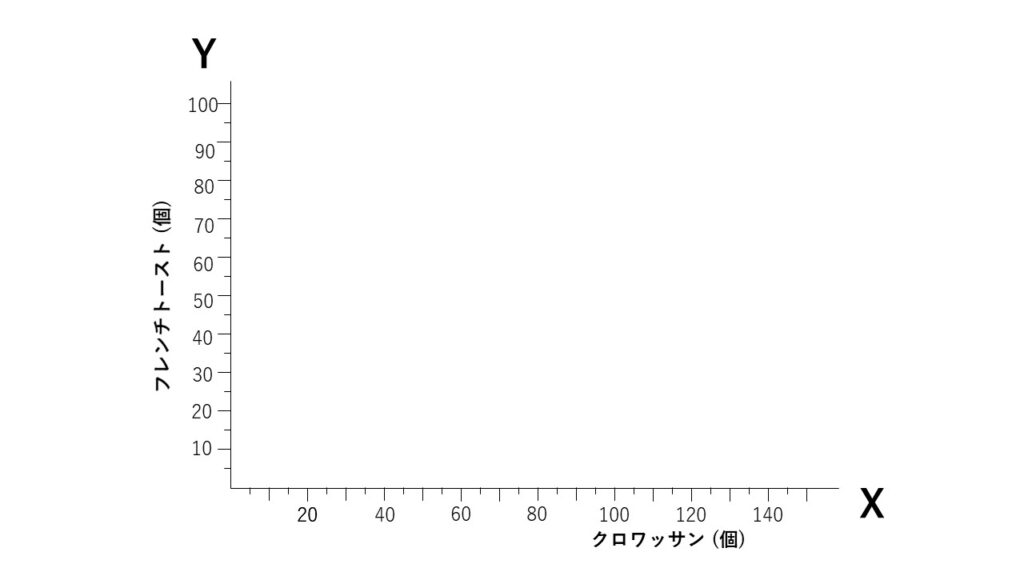
最初に、『１日あたりの焼く時間は420分以下でなければならない』という制約条件について考えてみましょう。

例題の条件に戻ると、クロワッサンとフレンチトースト１個を作るのに必要な作業時間（混ぜる時間・焼く時間）は以下の通りでした。

したがって、1日あたりに作るべきクロワッサンの個数をX、フレンチトーストの個数をYとすると、『3X + 6Y ≦ 420』という条件式が成り立ちます。これをグラフで示すと以下のようになります。

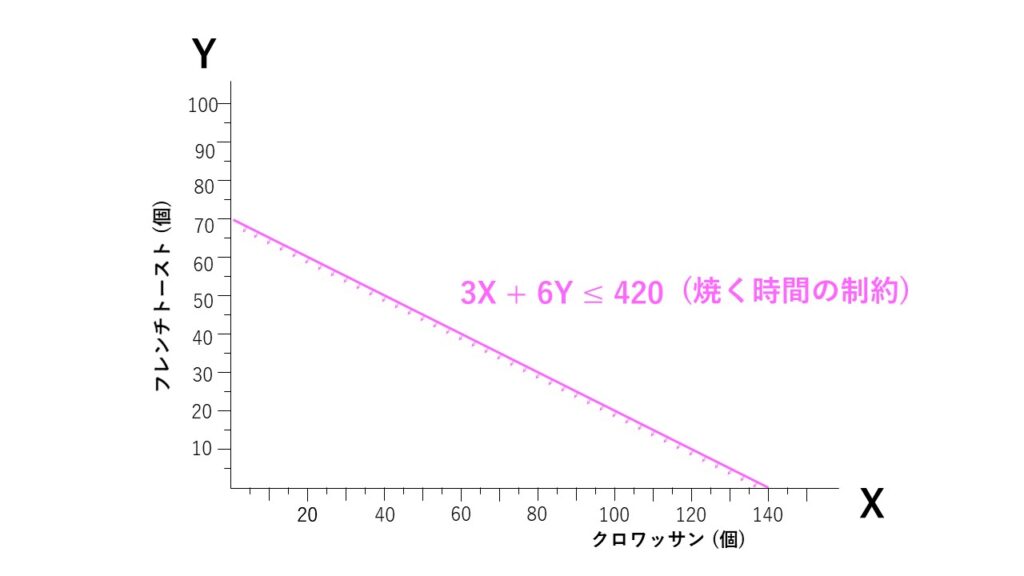
同様に、混ぜる時間の制約は『6X + 4.5Y ≦ 465』という条件式で表せます。これをグラフで示すと以下のようになります。

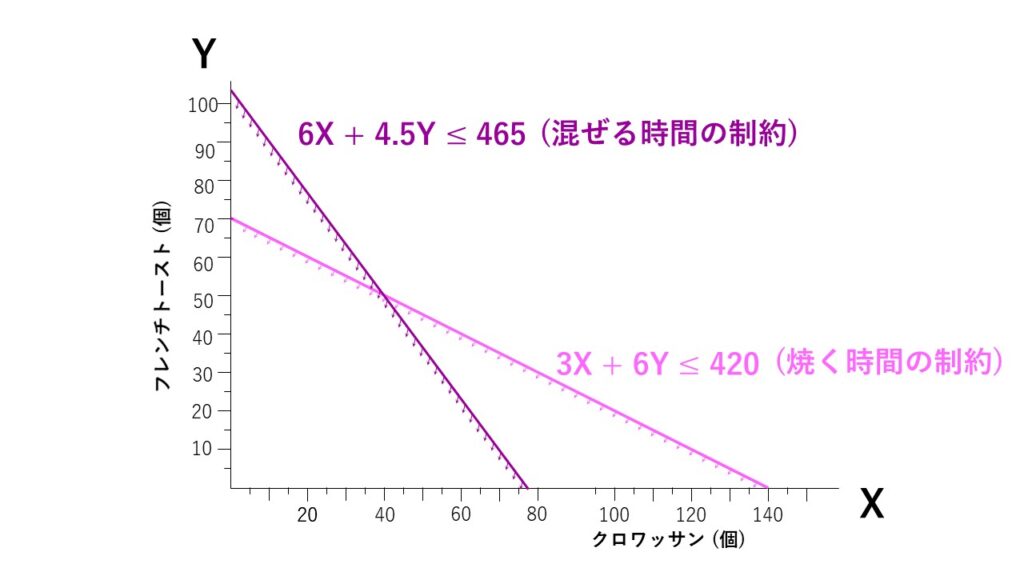
さらに、1日に売れるフレンチトーストの個数（需要）は60個までなので、作る数は60個以下にしなければなりません。つまり、条件式は『Y ≦ 60』で表せます。これをグラフで示すと以下になります。

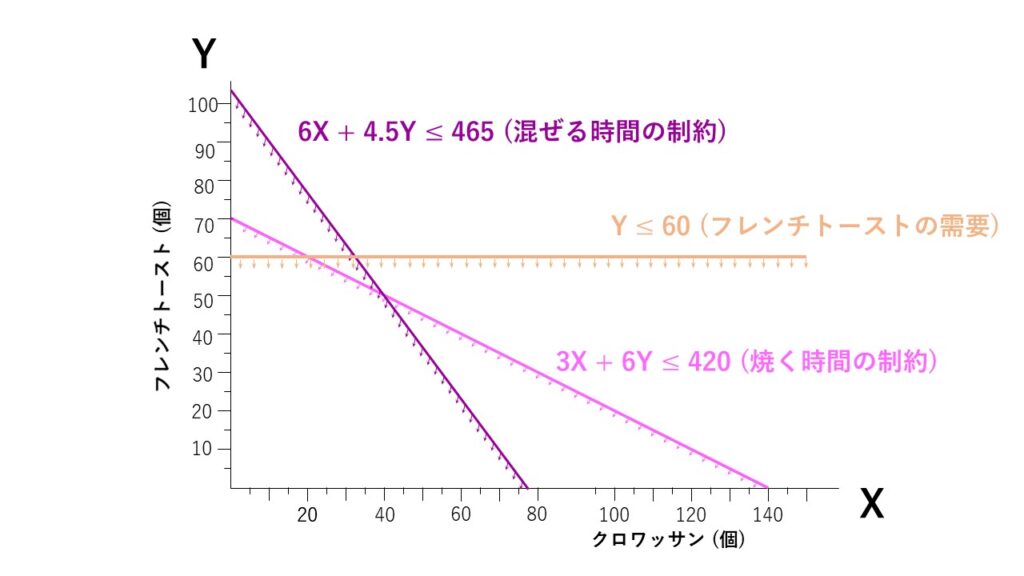
最後に、1日に売れるクロワッサンの個数（需要）は90個までなので、作る数は90個以下にしなければなりません。つまり、『X ≦ 90』という条件式で表せます。これをグラフで示すと以下になります。

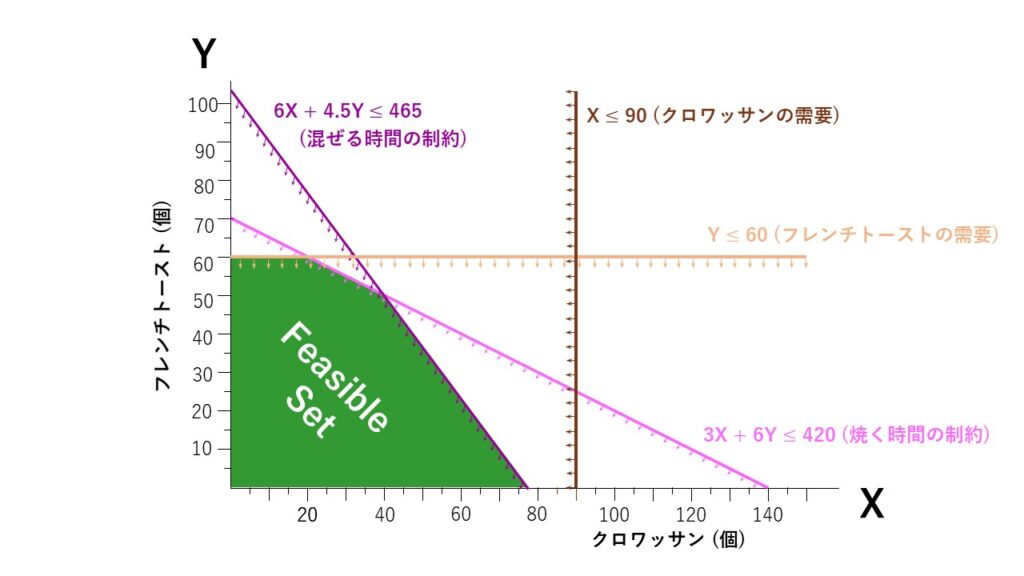
つまり、緑色で囲まれたエリアが、制約条件を満たす『クロワッサン（X）とフレンチトースト（Y）の個数の組み合わせ』 = 『Feasible Set』となります。

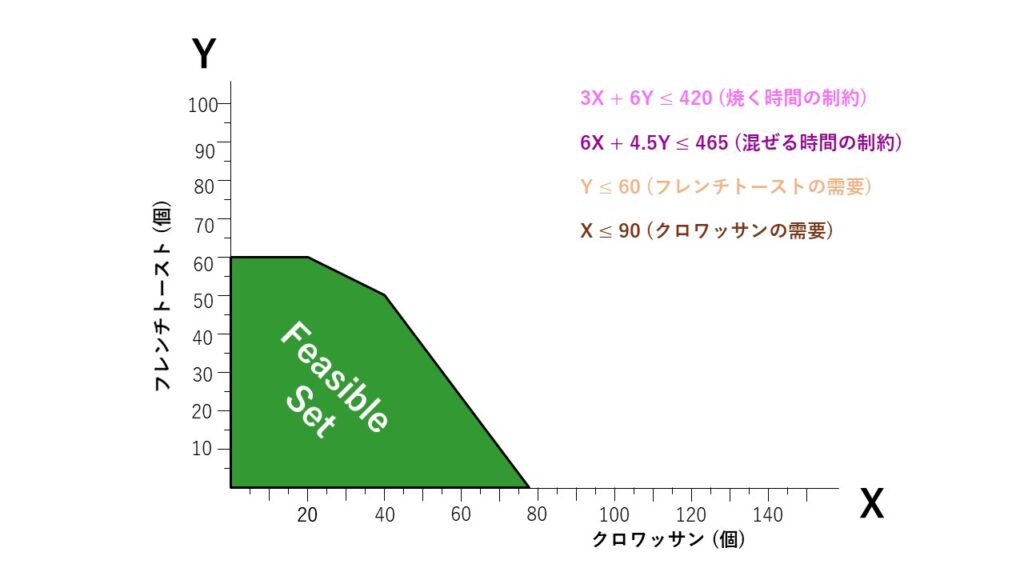
最終的に『求めたいもの』をグラフで表す

では、今回求めたいものである『合計の利益』はどのようにグラフで表せるでしょうか？クロワッサンを作る個数を（X）、フレンチトーストを作る個数を（Y）とすると、合計の利益は『50X ＋ 60Y』で定義できます。

仮に、合計の利益を1,500円としてみると、『50X ＋ 60Y = 1500』となり、以下の赤線のように示すことができます。

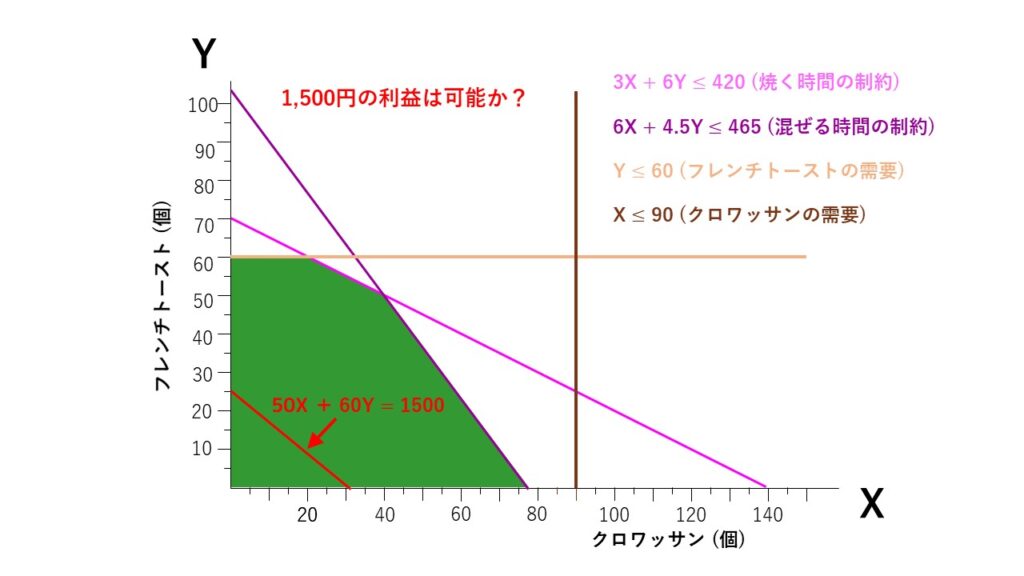
この場合、赤線は緑色のエリア内に含まれているので、制約条件内で『1500円の利益を出すことは可能』ということが分かります。

次に合計の利益を3,000円にしてみましょう。『50X ＋ 60Y = 3000』のグラフは以下のようになります。

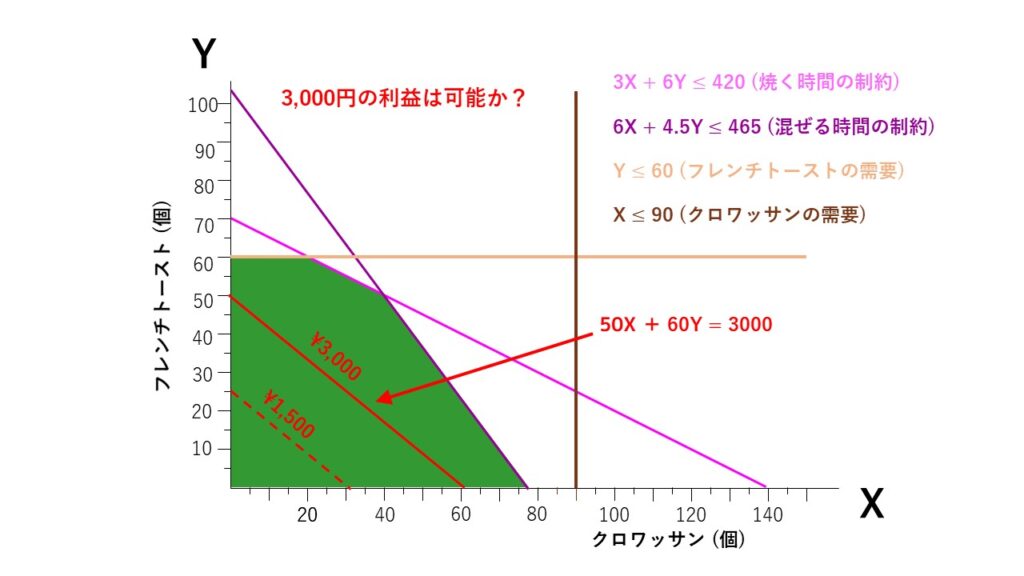
まだ赤線は緑色のエリア内に含まれているので、制約条件内で『3000円の利益を出すことは可能』ということが分かります。

今度は合計の利益を6,000円にしてみましょう。『50X ＋ 60Y = 6000』のグラフは以下のようになります。

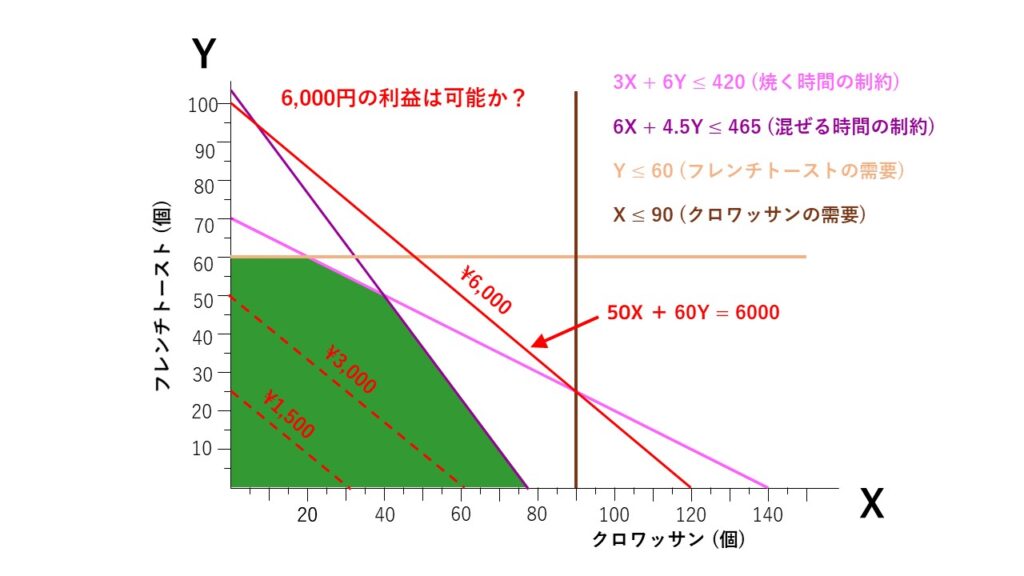
今度は赤線が緑色のエリアの外に出てしまいました。つまり、制約条件内で『6000円の利益を出すことは不可能』ということが分かりました。

では、最大の利益を出せるポイントはどこになるでしょうか？それは、緑色のエリアと赤線がぎりぎり接するポイントです。つまり、以下の通り『50X ＋ 60Y = 5000』のグラフがちょうど緑色のエリアと接することが分かります。

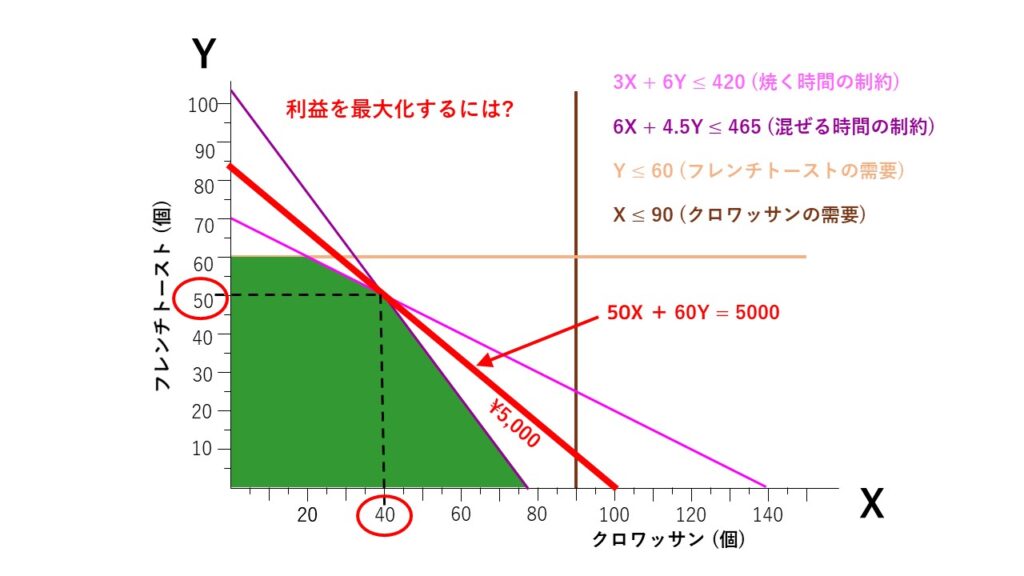
このときの接する点である（X=40, Y=50）が、それぞれ利益を最大化する『クロワッサンの個数 = 40』と『フレンチトーストの個数 = 50』になります。

解答レポートの解釈

ここからはソルバーのレポートの解説をします。まずは『解答レポート』を見てみましょう。

解答レポートには大きく３つのレポートが記載されています。『目的セル』と『変数セル』と『制約条件』についてです。

目的セルは、『求めたいもの（利益の合計）』を定義したD6セルのことです。ソルバー計算の結果、最大の利益である5000円が最終値になっていることが分かります。

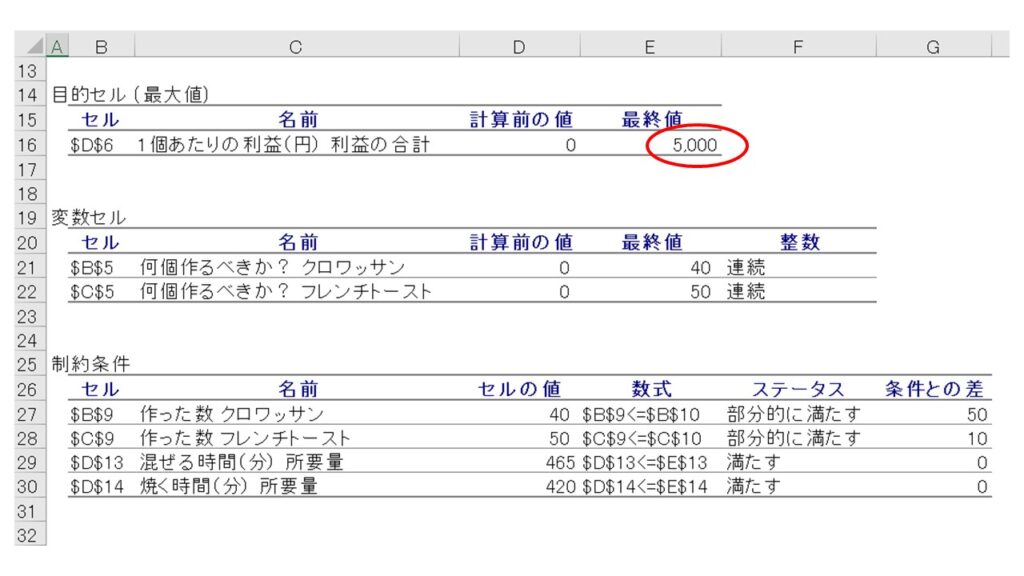
変数セルは、最初にステップ１で定義した変数のことです。つまり、クロワッサンとフレンチトーストを作る個数であるB5セルとC5セルが変数セルになります。ソルバー計算の結果、最大の利益を得るために作るべきクロワッサンとフレンチトーストの個数、つまり40個と50個が最終値となっています。

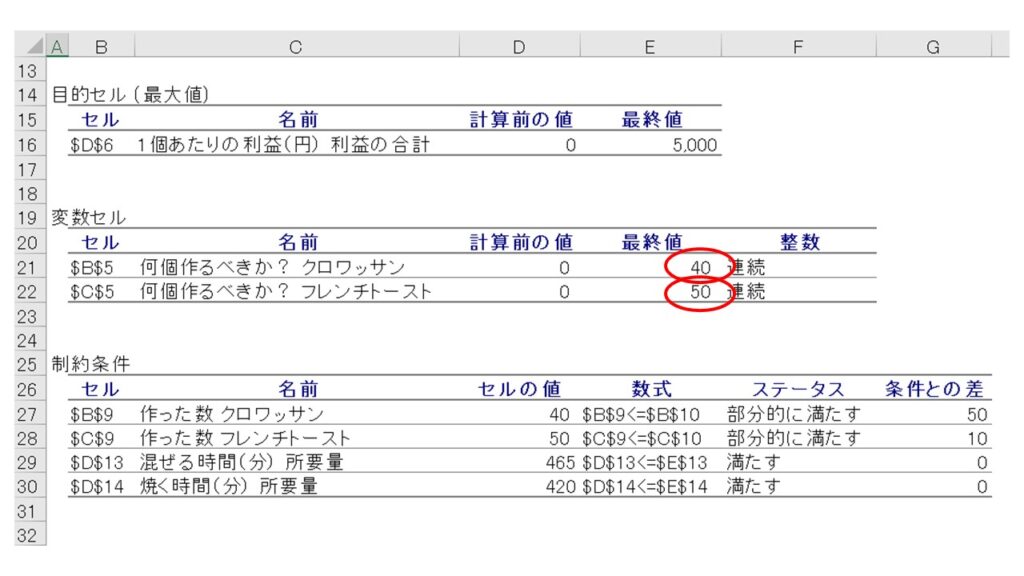
制約条件は、それぞれ入力した４つの制約条件が示されています。4つの制約条件に対応する条件式は以下の通りです。

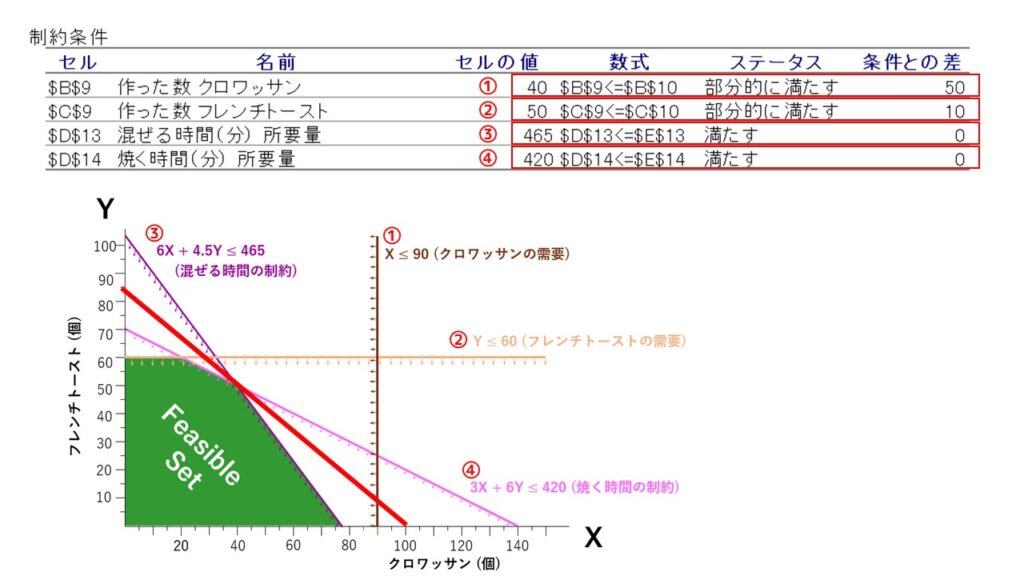
ステータスの項目について、③、④の制約条件のように『満たす』と表示されているものは、制約条件ギリギリまでリソースを使っているという意味になります。つまり、『混ぜる時間』と『焼く時間』の制約条件は、1日あたりのキャパシティである465分、420分ぎりぎりまで使われていることが分かります。

一方で、①、②の制約条件のステータスは『部分的に満たす』と表示されています。これは、ソルバー計算の結果、変数XとYが1日の需要数を下回る数（クロワッサン=40個 ＜ 90個、フレンチトースト50個 ＜ 60個）であることを示しています。

感度レポートの解釈

次に『感度レポート』の内容を解説します。感度レポートには非常に重要な情報が含まれていますので、ぜひ解説をしっかり読んで理解を深めて下さい。

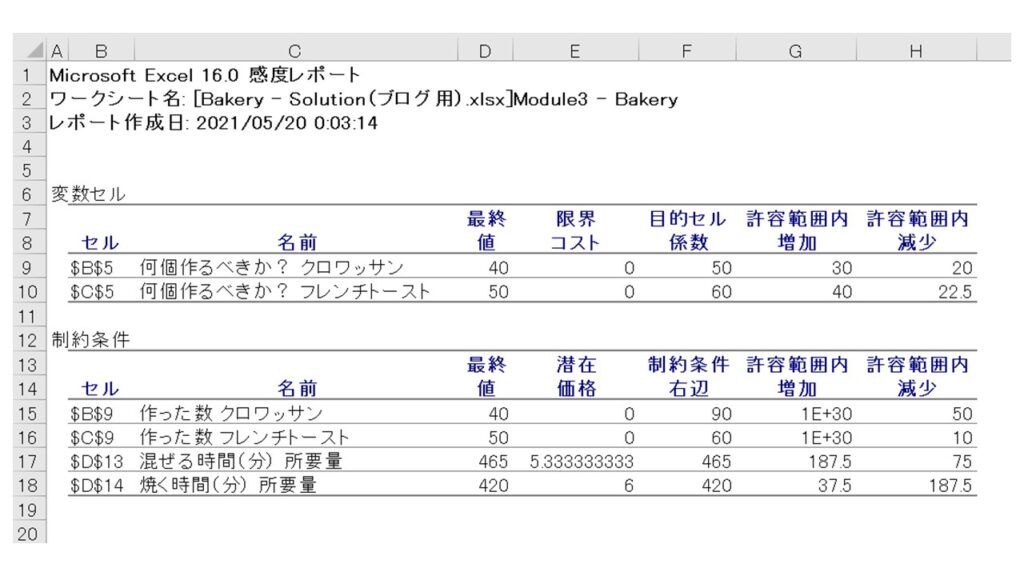
感度レポートには大きく２つのレポートが記載されています。『変数セル』と『制約条件』についてです。

変数セルについての解釈

変数セルには、『解答レポート』と同じように変数の最終値が示されています。（利益最大化するには、クロワッサン40個、フレンチトースト50個）

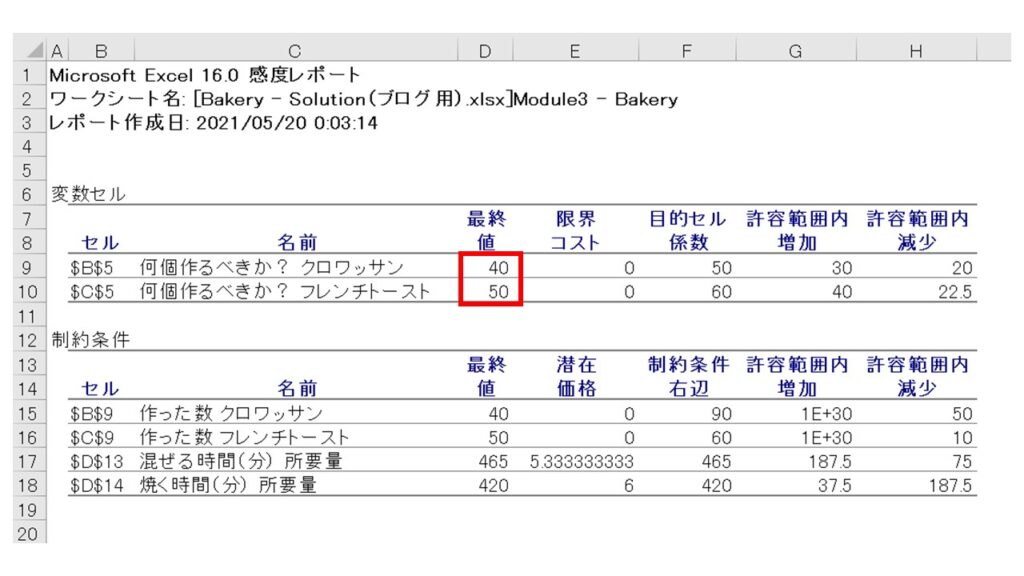
ここで大切なのは、『許容範囲内減少（増加）』の項目です。この項目の意味は、『1個あたりの利益がどこまで減っても（増えても）、変数の最終値は変わらないか？』を知ることができます。

下図の通り、クロワッサンの許容範囲内減少は『20』と示されています。これはつまり、現在クロワッサン1個あたりの利益は50円ですが、この利益が20円減って1個当たりの利益が30円になっても、『利益を最大化させるクロワッサンの個数（最終値）は変わらず40個である』ということを示しています。

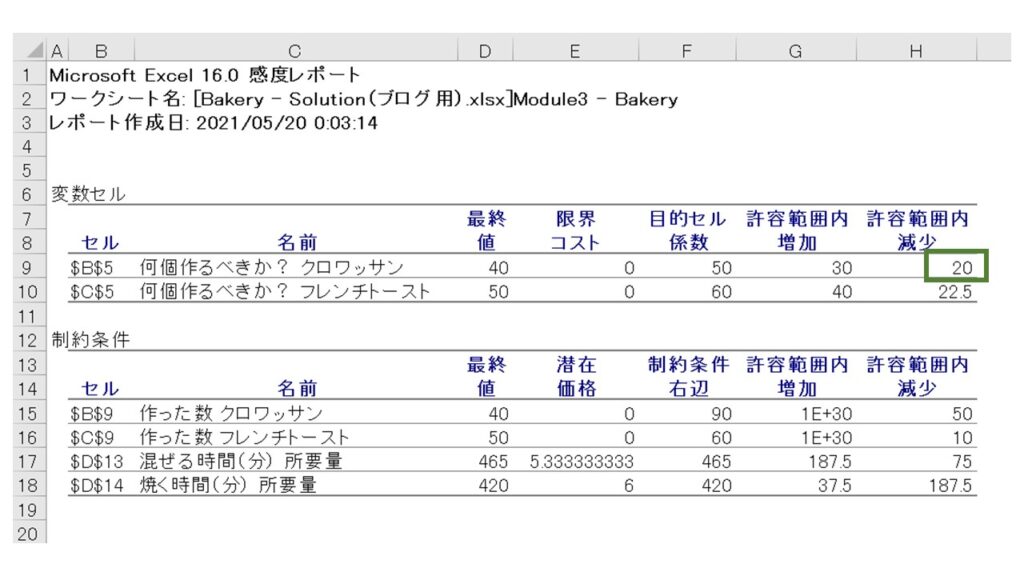
これはグラフで見るとどういうことでしょうか？クロワッサン1個あたりの利益が50円→30円になることは、利益を示す式である『50X + 60Y』が、『（50-20）X + 60Y』になることを表しています。したがって、下図の利益を示す直線である『赤線』が、『緑線』になることを表しています。

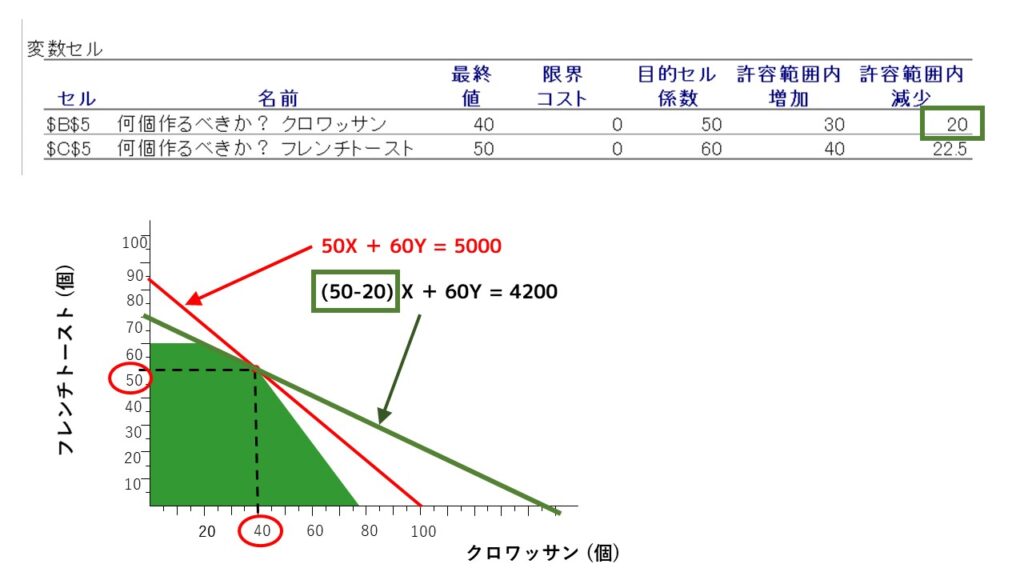
同じように、フレンチトーストの変数セル（C5セル）の許容範囲内減少は『22.5』円です。これはつまり、利益最大化するために作るべきフレンチトーストの個数は50個ですが、この50個という最適解はフレンチトースト1個あたりの利益が『22.5円』減少しても変わらないということを示しています。

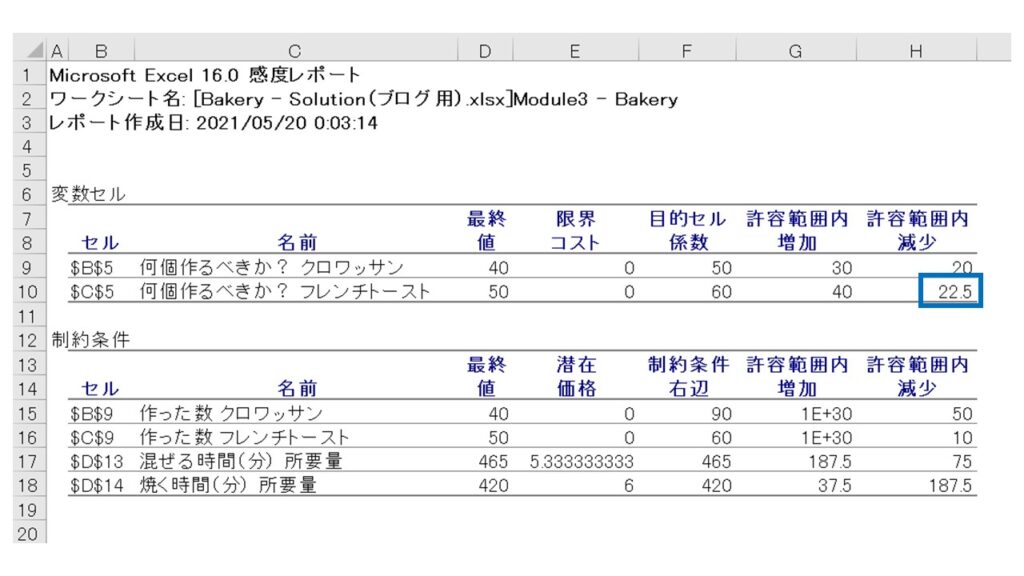
これをグラフで見ると以下のようになります。フレンチトースト1個あたりの利益が60円→37.5円になることは、利益を示す式である『50X + 60Y』が、『50X +（60-22.5）Y』になることを表しています。したがって、下図の利益を示す直線である『赤線』が、『青線』になることを表しています。

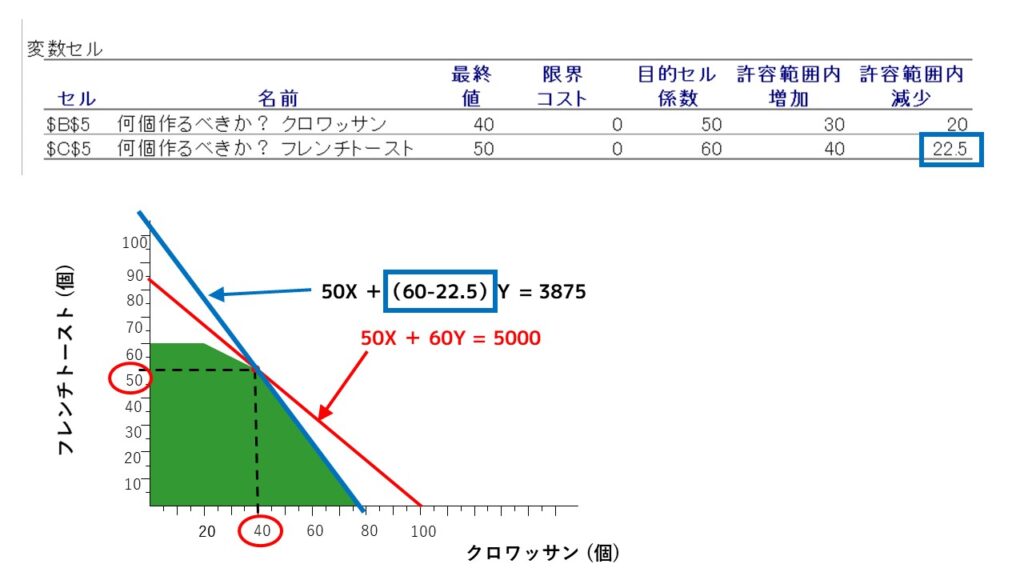
いかがでしょうか？これは実際のビジネスであなたが経営者の立場だった場合、『商品１個あたりの利益が変わった時』に意思決定をする有益な情報の１つになると思います。

制約条件と潜在価格についての解釈

最後に感度レポートの制約条件と『潜在価格』について解説します。制約条件の項目には、『解答レポート』と同じように条件式の最終値が示されています。（利益最大化するには、クロワッサン40個、フレンチトースト50個を作り、混ぜる時間は465分、焼く時間は420分を目一杯まで使う）

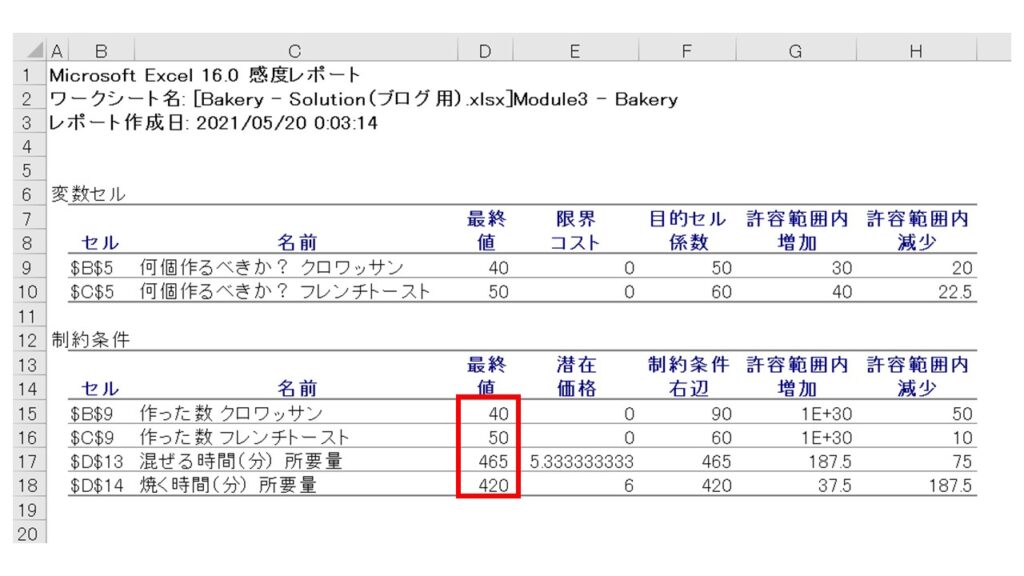
感度レポートで最も有益な情報は、『潜在価格』の項目です。この項目は、『制約条件のキャパシティを1単位追加すると、いくら利益が増加するか？』ということを表しています。

つまり、現在は1日あたりの混ぜる時間のキャパシティは465分が最大ですが、もしこのキャパシティを1分増加させれば、『利益は5.33円増加する』ということを示しています。

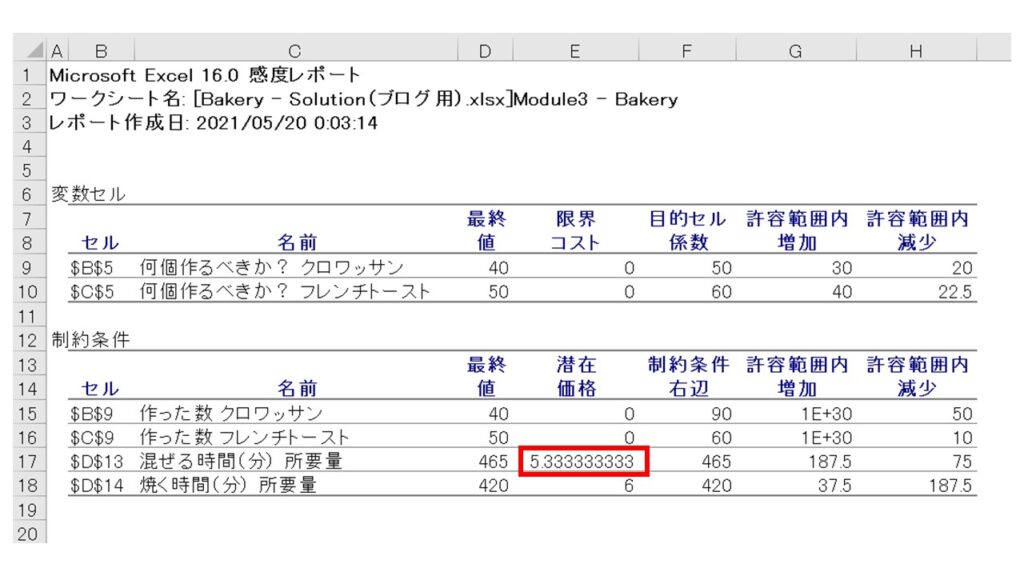
これはグラフで見るとどういうことでしょうか？1日あたり混ぜる時間のキャパシティ465分が1分増加するということは、混ぜる時間の制約条件式である『6X + 4.5Y ≤ 465』の右辺が、1ずつ増加する『6X + 4.5Y ≤ 465 +1』になることを表しています。したがって、右辺が増加するにつれ、下図の紫の直線が右に移動していきます。

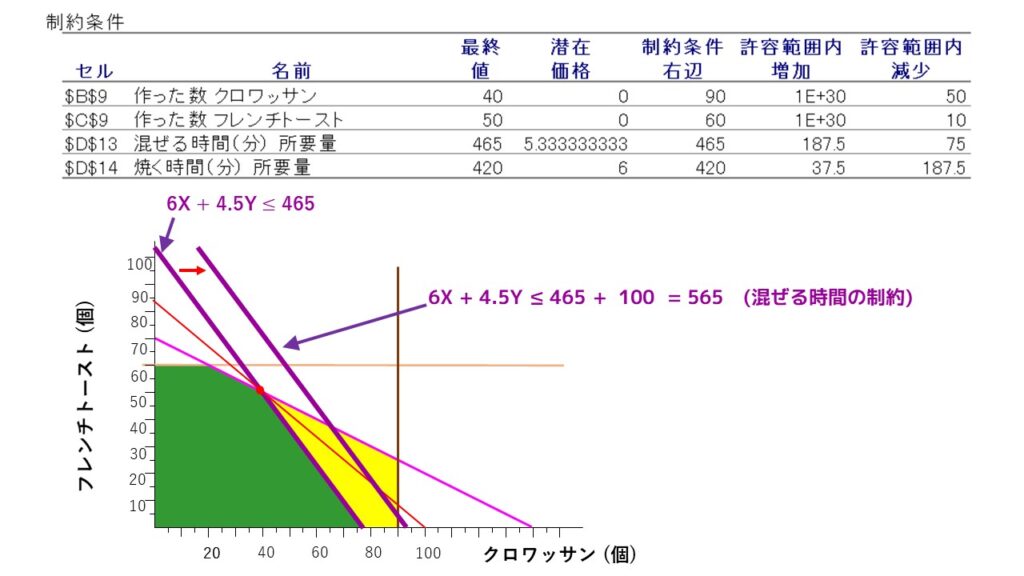
さらに、混ぜる時間の項目の『許容範囲内増加』を見ると、187.5と表示されています。これは、『潜在価格が適用できる範囲は、187.5分の増加まで』ということを示しています。つまり、混ぜる時間のキャパシティを1分増加させるごとに利益は5.33円増加するが、『この関係性が維持されるのは187.5分の増加分まで』ということです。

混ぜる時間のキャパシティを187.5分増価させたときにグラフはどうなっているかというと、以下のようになっています。

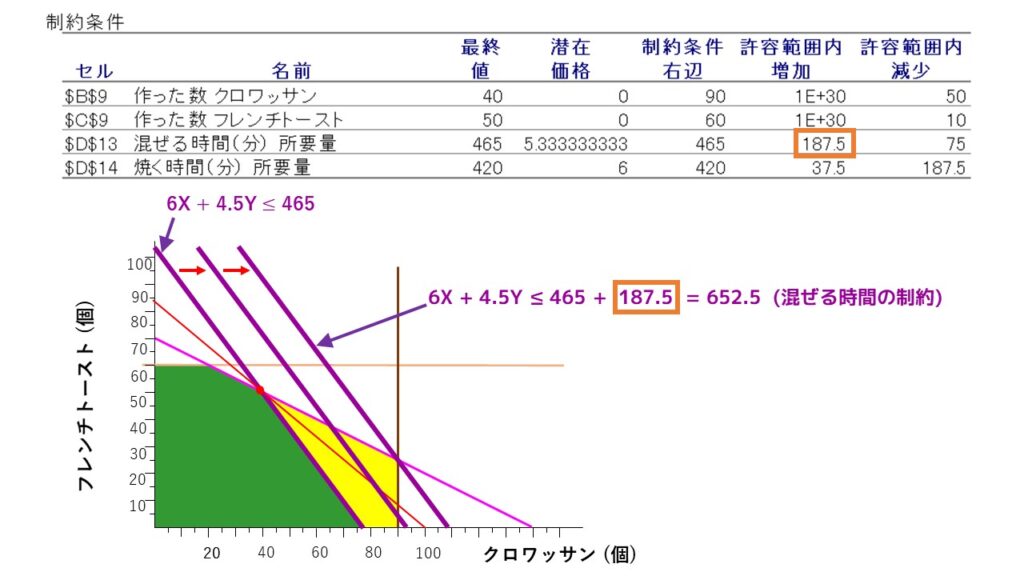
紫の直線が右に移動し続けて、ちょうど『X = 90』の直線と『3X + 6Y = 420』の直線の交点と交わったポイントになります。

いかがでしたでしょうか？『潜在価格』と『許容範囲内増加（減少）』の情報によって、キャパシティをいくら増加させると、利益がいくら増加するのかをシミュレーションできるようになりました。あなたが経営者であれば、この情報をもとに『キャパシティを増加させるための設備投資や人の雇用のコスト増』と『利益増』を比較して、意思決定をおこなうことができるようになります！

MBA流エクセル術【ソルバー編】まとめ

今回はMBA流エクセル術の第2弾として、MBAで教えられるソルバーの基本操作やレポートの解釈方法を解説してきました。（UC San Diego のMBAで実際に教えられている授業の前半部分に当たります）いかがでしたでしょうか？改めて紹介したものをまとめると以下になります。

この記事が少しでもみなさんのお役に立つことを願っております！

この記事では４つの例題をもとに解説してきました。おそらく初心者がソルバーで躓くポイントは、『どのように条件設定したら良いか？』という所だと思います。当ブログの補足として、以下の参考書がおすすめです。実際の操作方法、手順、解説に的を絞っているので、ソルバーの基本操作を確実にマスターできます！

新版 Excelでできる最適化の実践らくらく読本?ソルバーで自由自在に解く

MBA留学を目指されている方は、以下の記事をぜひ参考にしてみて下さいね。

【海外MBA受験】TOEFL68点から合格までの全ステップまとめ

MBA社費留学：倍率60倍の社内選考を突破した小論文を公開

MBAまでの道のり（TOEFL全般、Reading編）

Twitterでも定期的にMBA関連・Eコマースの情報配信をしているので、ぜひフォローをお願いします！